PageRank란?
PageRank는 하이퍼링크 구조를 가지는 문서에 상대적 중요도에 따라 가중치를 부여하는 방법이다.
PageRank Algorithm은 더 중요한 페이지가 더 많은 사이트로부터 링크를 받는다는 것에 비롯되었는데,
만약에 page A, B, C, D 가 있을 때 page A에서 원하는 결과를 찾지 못해서 page B로 방문했을 경우
page B는 임의의 확률 x 1/3 만큼의 pagerank를 받게 된다.
이렇게 PageRank 값을 page 간에 주고받는 것을 반복하다 보면, 전체 웹 페이지가
특정한 PageRank값에 수렴하는데, 이를 통해 최종 PageRank값을 계산할 수 있다.
식으로 나타내면,
초기 PageRank r 을 설정하고, 인접 행렬(각 page 간 방문 빈도) L을 구했을 때,
L * r 을 r이 특정 vector로 수렴하게 될 때까지 하면
수렴된 값이 최종 PageRank가 된다.
이 과정은 밑에서 더 자세히 살펴보도록 하자.
예시. Google matrix
구글 행렬은 구글의 창립자 래리 페이지가 만든 구글의 PageRank algorithm에서 사용되는 확률론적 matrix인데,
아주 간단히 말하자면
위의 "임의의 확률" 을 감쇠 계수(damping factor)로 두고 0.85로 사용하는 방식이다.
현재까지도 구글에서 사용되고 있기 때문에 PageRank 분야에서 아주 유명하다고 볼 수 있다.
그럼 이제 본격적으로 numpy 에서 PageRank를 구하는 법을 살펴보도록 하자!
1. page graph
우리가 구해야할 것은 결론적으로 PageRank를 이용하여 중요한 page를 찾은 뒤
검색 결과를 출력할 때 그들의 우선순위를 높이는 것이기 때문에,
networks에 기반해 page들의 관계를 찾아야 한다.
우리는 이 관계들을 인접 행렬로 구할텐데
먼저 node와 edge로 구성된 network를 살펴보자.
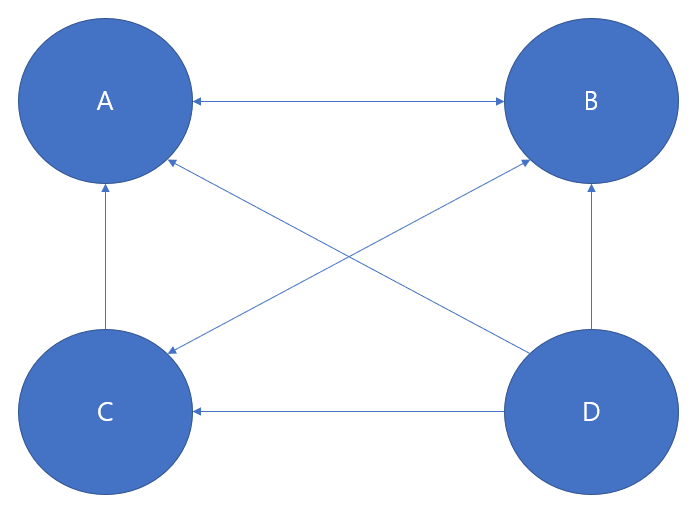
위 그림은 Page A, B, C, D의 관계이다.
이 그림을 보고 각 node(page)가 다른 node에게 나누어줄 점수를 구할 수 있다.
이 점수는 자신의 기본 점수(1)를 자신이 보내는 links의 개수만큼 나눠주면 된다.
따라서 위 그래프에 따른 나눠줄 자신의 점수는
- A : link가 1개이므로 1
- B : 2개이므로 1/2
- C : B와 동일
- D : 3개이므로 1/3
이를 numpy array를 사용해 4x4 인접 행렬로 나타내면

(A, B, C, D 순서의 인접 행렬입니다!)
2. eigenvector, value를 사용하여 pagerank 구하기
이 방법은 eigenvector를 사용해 빠르게 pagerank를 구하는 방법인데,
eigenvalue가 1인 eigenvector를 사용하면 인접 행렬 L을 가지고 아주 쉽게 구할 수 있다.
즉, pagerank 자체가 특정 vector로 수렴하는 vector 이므로
r = Lr에 대한 r이 value가 1인 수렴하는 eigenvector라 생각하는 것이다. (찾느라 힘들었다... ㅠ)
(출처 : http://statweb.stanford.edu/)
구하는 순서는 다음과 같다.
- L의 eigenvector, value를 구한다.
- Eigenvalue의 절댓값 중 가장 큰 값과 상응하는 eigenvector를 찾는다.
- pagerank r = 100*eigenvector(normalized vector)
설명이 좀 지루하니 코드로 바로 넘어가 보자

이렇게 r을 구할 수 있다.
3. 반복을 통해 PageRank 구하기
이번엔 이론 그대로~ 수렴할 때까지 반복을 하여 PageRank를 구해보자.
1. 식 : r = L * r
2. 초기값 : 이미 matrix L은 구했으므로 vector r의 초기값을 설정해야 한다.
vector r의 초기값은 100/(page의 개수)라고 잡아보자.
3.update : 이제 L*r의 update 과정만 거치면 되는데 반복 실행해야 하므로while문안에서 계속 L*r을 해주고, while문의 조건에 이전 r과 현재 r의 차이가 0.01보다 작으면 false를 반환하도록 하자
아래 코드를 살펴보자

위 코드에서 while 문 앞에서 r = L @ r (update)을 한번 해줘야 합니다!
아까 2번에서 구한 PageRank와 거의 비슷한 값이 나온 것을 확인할 수 있다.
(오차는 소수점 연산에서 발생하였습니다!)
'Artificial Intelligence' 카테고리의 다른 글
| [numpy] 5주차 eigen vector, value (0) | 2020.04.15 |
|---|---|
| [numpy] 5주차 PIL로 image 읽고 변환하기 (0) | 2020.04.15 |
| [numpy] 4주차 gram-schmidt, reflection matrix (2) | 2020.04.09 |
| [numpy] 3주차 transform, determinant (0) | 2020.03.25 |
| [numpy] 2주차 기본 행렬 연산과 인덱싱 (1) | 2020.03.23 |
PageRank란?
PageRank는 하이퍼링크 구조를 가지는 문서에 상대적 중요도에 따라 가중치를 부여하는 방법이다.
PageRank Algorithm은 더 중요한 페이지가 더 많은 사이트로부터 링크를 받는다는 것에 비롯되었는데,
만약에 page A, B, C, D 가 있을 때 page A에서 원하는 결과를 찾지 못해서 page B로 방문했을 경우
page B는 임의의 확률 x 1/3 만큼의 pagerank를 받게 된다.
이렇게 PageRank 값을 page 간에 주고받는 것을 반복하다 보면, 전체 웹 페이지가
특정한 PageRank값에 수렴하는데, 이를 통해 최종 PageRank값을 계산할 수 있다.
식으로 나타내면,
초기 PageRank r 을 설정하고, 인접 행렬(각 page 간 방문 빈도) L을 구했을 때,
L * r 을 r이 특정 vector로 수렴하게 될 때까지 하면
수렴된 값이 최종 PageRank가 된다.
이 과정은 밑에서 더 자세히 살펴보도록 하자.
예시. Google matrix
구글 행렬은 구글의 창립자 래리 페이지가 만든 구글의 PageRank algorithm에서 사용되는 확률론적 matrix인데,
아주 간단히 말하자면
위의 "임의의 확률" 을 감쇠 계수(damping factor)로 두고 0.85로 사용하는 방식이다.
현재까지도 구글에서 사용되고 있기 때문에 PageRank 분야에서 아주 유명하다고 볼 수 있다.
그럼 이제 본격적으로 numpy 에서 PageRank를 구하는 법을 살펴보도록 하자!
1. page graph
우리가 구해야할 것은 결론적으로 PageRank를 이용하여 중요한 page를 찾은 뒤
검색 결과를 출력할 때 그들의 우선순위를 높이는 것이기 때문에,
networks에 기반해 page들의 관계를 찾아야 한다.
우리는 이 관계들을 인접 행렬로 구할텐데
먼저 node와 edge로 구성된 network를 살펴보자.

위 그림은 Page A, B, C, D의 관계이다.
이 그림을 보고 각 node(page)가 다른 node에게 나누어줄 점수를 구할 수 있다.
이 점수는 자신의 기본 점수(1)를 자신이 보내는 links의 개수만큼 나눠주면 된다.
따라서 위 그래프에 따른 나눠줄 자신의 점수는
- A : link가 1개이므로 1
- B : 2개이므로 1/2
- C : B와 동일
- D : 3개이므로 1/3
이를 numpy array를 사용해 4x4 인접 행렬로 나타내면

(A, B, C, D 순서의 인접 행렬입니다!)
2. eigenvector, value를 사용하여 pagerank 구하기
이 방법은 eigenvector를 사용해 빠르게 pagerank를 구하는 방법인데,
eigenvalue가 1인 eigenvector를 사용하면 인접 행렬 L을 가지고 아주 쉽게 구할 수 있다.
즉, pagerank 자체가 특정 vector로 수렴하는 vector 이므로
r = Lr에 대한 r이 value가 1인 수렴하는 eigenvector라 생각하는 것이다. (찾느라 힘들었다... ㅠ)
(출처 : http://statweb.stanford.edu/)
구하는 순서는 다음과 같다.
- L의 eigenvector, value를 구한다.
- Eigenvalue의 절댓값 중 가장 큰 값과 상응하는 eigenvector를 찾는다.
- pagerank r = 100*eigenvector(normalized vector)
설명이 좀 지루하니 코드로 바로 넘어가 보자

이렇게 r을 구할 수 있다.
3. 반복을 통해 PageRank 구하기
이번엔 이론 그대로~ 수렴할 때까지 반복을 하여 PageRank를 구해보자.
1. 식 : r = L * r
2. 초기값 : 이미 matrix L은 구했으므로 vector r의 초기값을 설정해야 한다.
vector r의 초기값은 100/(page의 개수)라고 잡아보자.
3.update : 이제 L*r의 update 과정만 거치면 되는데 반복 실행해야 하므로while문안에서 계속 L*r을 해주고, while문의 조건에 이전 r과 현재 r의 차이가 0.01보다 작으면 false를 반환하도록 하자
아래 코드를 살펴보자

위 코드에서 while 문 앞에서 r = L @ r (update)을 한번 해줘야 합니다!
아까 2번에서 구한 PageRank와 거의 비슷한 값이 나온 것을 확인할 수 있다.
(오차는 소수점 연산에서 발생하였습니다!)
'Artificial Intelligence' 카테고리의 다른 글
| [numpy] 5주차 eigen vector, value (0) | 2020.04.15 |
|---|---|
| [numpy] 5주차 PIL로 image 읽고 변환하기 (0) | 2020.04.15 |
| [numpy] 4주차 gram-schmidt, reflection matrix (2) | 2020.04.09 |
| [numpy] 3주차 transform, determinant (0) | 2020.03.25 |
| [numpy] 2주차 기본 행렬 연산과 인덱싱 (1) | 2020.03.23 |
