오늘은 그람 슈미트 직교화와 반사 행렬에 대해 알아보자.
1. gram-schmidt 직교화
우선 gram-schmidt 직교화의 의미를 위키백과에 검색해보면
"내적 공간에서 유한 개의 일차 독립 벡터 집합을 정규 직교 기저로 변환하는 방법이다"
라 한다.
(출처 : https://ko.wikipedia.org/wiki/%EA%B7%B8%EB%9E%8C-%EC%8A%88%EB%AF%B8%ED%8A%B8_%EA%B3%BC%EC%A0%95)
의미를 조금 해석해보자면,
1) 일차독립 벡터 집합은 벡터 집합 내의 모든 벡터들이
남은 다른 벡터들의 일차 결합으로 나타낼 수 없는 벡터들의 집합을 의미하는데
여기서 일차 결합이란, 벡터들과의 사칙연산을 말한다.
따라서 예를 들어 v = [[1,0,0], [0,1,0], [0,0,1]]라는 단위행렬이 있을 때
각각의 벡터들은 나머지 벡터들끼리 어떠한 연산을 취해도 그 벡터를 만들 수 없게 된다.
따라서 v는 일차 독립 벡터 집합이다.
2) 정규 직교 기저(orthonormal basis)는 벡터 집합 내 벡터들을 갖고, 어떤 두 벡터를 골라 내적을 하였을 때 결과가 0이 나오면서, 각 벡터의 크기가 1이 되는 벡터들의 집합을 말하며
이는 각 벡터들이 서로 직교하는 상태임을 의미한다.
그렇다면 왜 정규 직교 기저가 필요한가?
- 정규 직교 기저는 vector 간의 어떠한 변화(reflection, transform)등을 할 때 계산을 아주 쉽게 만들어주기 때문이다.(밑에 reflection matrix를 구할 때 알 수 있습니다)
구현
이제 각설하고, gram-schmidt 직교화 방법에 대해 알아보자.
벡터의 집합 v = {v1, v2,..., vn}이 있다고 할 때
정규 직교 기저(orthogonal basis)를 구하는 법은 다음과 같다.

이렇게 계산된 e가 정규 직교 기저가 되는 것이다!
numpy 코드로 알아보자.

2. reflection matrix
이제 우리는 gram-schmidt 과정을 거쳐 만든 정규 직교 기저를 이용하여
reflection matrix를 구할 차례이다.
그전에 reflection이 되었는지, 안되었는지 확인하기 힘들기 때문에
벡터들을 화살표로 나타내고, 곰을 만들어 전, 후 과정을 살펴보려 한다.
* 곰 모양 함수 가져오기
이 곳에 가면 bearNecessities.py 파일을 받을 수 있다.
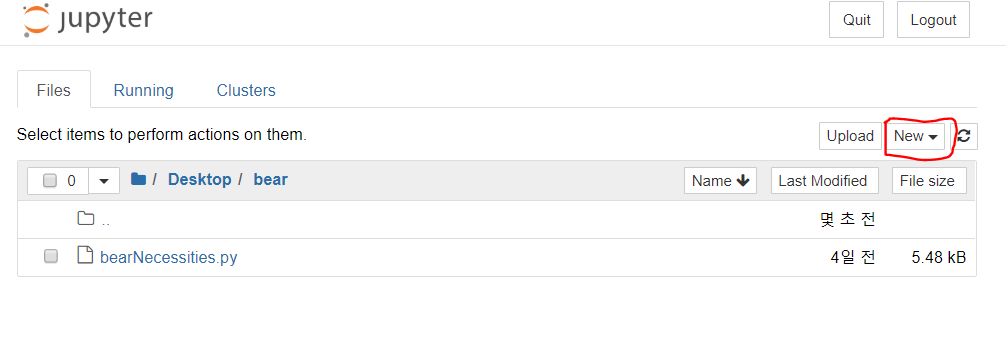
이후 받은 파일을 아무 폴더에 넣는다.
그냥 파이참을 사용하시는 분은 그냥 폴더 내에 py 파일을 하나 생성하면 되고,
주피터 노트북을 사용하면, 우측 상단의 new 버튼을 눌러 python 3을 누르면 py 파일이 생긴다!
이제 실행 환경이 갖춰졌다면
reflection matrix가 무엇인지 살펴보자!
reflection이란?
임의의 matrix v가 있을 때 v에 대해 마치 거울에 반사한 것처럼 v'를 만드는 것이다.
과정
- reflection이 된 v'은 다른 basis에 있기 때문에 처음에 v에 대한 정규 직교(orthonormal) E를 구한다.
- 이후 v에서 v'로의 basis 변환을 하기 위해 E의 역행렬을 곱하고
- 원하는 방향으로의 transform matrix을 곱한다.
- 그리고 다시 E를 곱해주면 v의 reflection matrix가 만들어진다.
transform matrix는 방향에 따라 천차만별인데
대표적으로 2차원에서
1. x축에 대한 반사의 행렬 T = [[1, 0], [0, -1]]
2. y축에 대한 반사의 행렬 T = [[-1, 0], [0, 1]]
이 있다. (직접 아무 행렬 만들어서 곱해보면 대칭이 되는 것을 볼 수 있습니다!)
그럼 이제 numpy와 곰을 이용해 reflection이 되는 것을 보도록 하자!

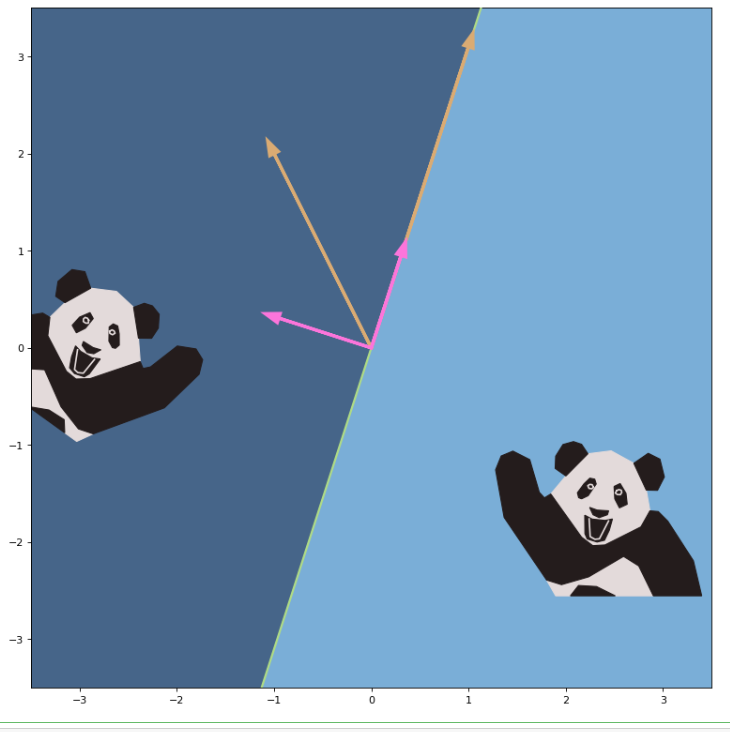
이처럼 대칭이 된 것을 볼 수 있겠다. (몇 번 봐도 귀엽군..)
궁금한 점, 잘못된 부분이 있다면 댓글 남겨주세요!
'Artificial Intelligence' 카테고리의 다른 글
| [numpy] 5주차 eigen vector, value (0) | 2020.04.15 |
|---|---|
| [numpy] 5주차 PIL로 image 읽고 변환하기 (0) | 2020.04.15 |
| [numpy] 3주차 transform, determinant (0) | 2020.03.25 |
| [numpy] 2주차 기본 행렬 연산과 인덱싱 (1) | 2020.03.23 |
| [numpy] 1주차 numpy 기초 함수 및 행렬 변환 정리 (1) | 2020.03.19 |
오늘은 그람 슈미트 직교화와 반사 행렬에 대해 알아보자.
1. gram-schmidt 직교화
우선 gram-schmidt 직교화의 의미를 위키백과에 검색해보면
"내적 공간에서 유한 개의 일차 독립 벡터 집합을 정규 직교 기저로 변환하는 방법이다"
라 한다.
(출처 : https://ko.wikipedia.org/wiki/%EA%B7%B8%EB%9E%8C-%EC%8A%88%EB%AF%B8%ED%8A%B8_%EA%B3%BC%EC%A0%95)
의미를 조금 해석해보자면,
1) 일차독립 벡터 집합은 벡터 집합 내의 모든 벡터들이
남은 다른 벡터들의 일차 결합으로 나타낼 수 없는 벡터들의 집합을 의미하는데
여기서 일차 결합이란, 벡터들과의 사칙연산을 말한다.
따라서 예를 들어 v = [[1,0,0], [0,1,0], [0,0,1]]라는 단위행렬이 있을 때
각각의 벡터들은 나머지 벡터들끼리 어떠한 연산을 취해도 그 벡터를 만들 수 없게 된다.
따라서 v는 일차 독립 벡터 집합이다.
2) 정규 직교 기저(orthonormal basis)는 벡터 집합 내 벡터들을 갖고, 어떤 두 벡터를 골라 내적을 하였을 때 결과가 0이 나오면서, 각 벡터의 크기가 1이 되는 벡터들의 집합을 말하며
이는 각 벡터들이 서로 직교하는 상태임을 의미한다.
그렇다면 왜 정규 직교 기저가 필요한가?
- 정규 직교 기저는 vector 간의 어떠한 변화(reflection, transform)등을 할 때 계산을 아주 쉽게 만들어주기 때문이다.(밑에 reflection matrix를 구할 때 알 수 있습니다)
구현
이제 각설하고, gram-schmidt 직교화 방법에 대해 알아보자.
벡터의 집합 v = {v1, v2,..., vn}이 있다고 할 때
정규 직교 기저(orthogonal basis)를 구하는 법은 다음과 같다.

이렇게 계산된 e가 정규 직교 기저가 되는 것이다!
numpy 코드로 알아보자.

2. reflection matrix
이제 우리는 gram-schmidt 과정을 거쳐 만든 정규 직교 기저를 이용하여
reflection matrix를 구할 차례이다.
그전에 reflection이 되었는지, 안되었는지 확인하기 힘들기 때문에
벡터들을 화살표로 나타내고, 곰을 만들어 전, 후 과정을 살펴보려 한다.
* 곰 모양 함수 가져오기
이 곳에 가면 bearNecessities.py 파일을 받을 수 있다.

이후 받은 파일을 아무 폴더에 넣는다.
그냥 파이참을 사용하시는 분은 그냥 폴더 내에 py 파일을 하나 생성하면 되고,
주피터 노트북을 사용하면, 우측 상단의 new 버튼을 눌러 python 3을 누르면 py 파일이 생긴다!
이제 실행 환경이 갖춰졌다면
reflection matrix가 무엇인지 살펴보자!
reflection이란?
임의의 matrix v가 있을 때 v에 대해 마치 거울에 반사한 것처럼 v'를 만드는 것이다.
과정
- reflection이 된 v'은 다른 basis에 있기 때문에 처음에 v에 대한 정규 직교(orthonormal) E를 구한다.
- 이후 v에서 v'로의 basis 변환을 하기 위해 E의 역행렬을 곱하고
- 원하는 방향으로의 transform matrix을 곱한다.
- 그리고 다시 E를 곱해주면 v의 reflection matrix가 만들어진다.
transform matrix는 방향에 따라 천차만별인데
대표적으로 2차원에서
1. x축에 대한 반사의 행렬 T = [[1, 0], [0, -1]]
2. y축에 대한 반사의 행렬 T = [[-1, 0], [0, 1]]
이 있다. (직접 아무 행렬 만들어서 곱해보면 대칭이 되는 것을 볼 수 있습니다!)
그럼 이제 numpy와 곰을 이용해 reflection이 되는 것을 보도록 하자!


이처럼 대칭이 된 것을 볼 수 있겠다. (몇 번 봐도 귀엽군..)
궁금한 점, 잘못된 부분이 있다면 댓글 남겨주세요!
'Artificial Intelligence' 카테고리의 다른 글
| [numpy] 5주차 eigen vector, value (0) | 2020.04.15 |
|---|---|
| [numpy] 5주차 PIL로 image 읽고 변환하기 (0) | 2020.04.15 |
| [numpy] 3주차 transform, determinant (0) | 2020.03.25 |
| [numpy] 2주차 기본 행렬 연산과 인덱싱 (1) | 2020.03.23 |
| [numpy] 1주차 numpy 기초 함수 및 행렬 변환 정리 (1) | 2020.03.19 |
