저번 시간에는 행렬 간의 기본적인 연산과 인덱싱에 대해 알아보았었다.
따라서 이번에는 저번 시간에 배운 기본적인 연산을 이용해
행렬 변환과 행렬식을 구하는 방법에 대해 글을 써보려 한다.
1. vector를 가지고 행렬 transformation 하기
임의의 벡터 x를 가지고 어떤 행렬 A에 대해 transformation을 하는 방법은 간단하다.
단, 벡터와 행렬의 공간이 맞아야 한다. (벡터 공간의 수와 행렬의 행)
예시를 보자

3 x 3 행렬 A에 대해 (1,2,3)으로 정의된 vector x의 transformation을 나타내려면
행렬 A의 각 행에 대해서 vector를 내적 하면 된다.
하지만 좀 보기 불편해 보인다.
사실 transformation을 하는데에 따로 함수를 정의할 필요는 없다.

그냥 내적 해도 같은 결과가 나오기 때문이다.
이는 vector에서 행렬로 transformation을 하던,
행렬에서 행렬로 하던 똑같은 결과가 나올 것을 암시한다.
행렬 -> 행렬로 transform을 하면
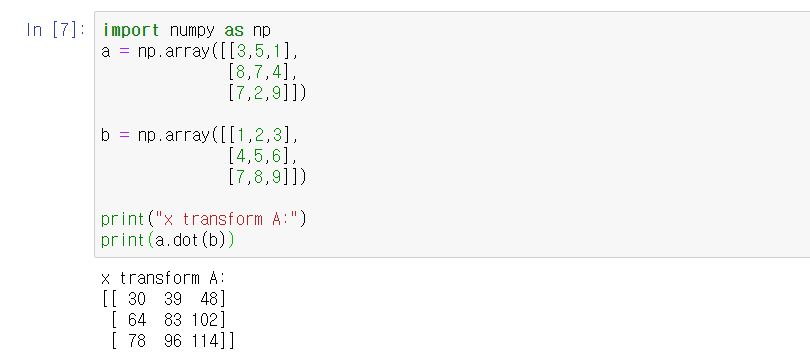
이러한 결과가 나온다.
어라? 이게 무슨 소리지?
이건 내적이지 transform이 아니잖아요!
벡터 간의 내적을 풀어보자면
임의의 벡터 u, v가 있을 때 벡터 u와 v를 내적 한 것은
u를 transpose 시키고 벡터 v와 벡터 곱을 한 것과 같다.
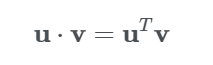
따라서 내적 = transform 이 되는 것이다.
(위키피디아에서 해석해본 결과 이런 것 같은데 저도 정확히 이게 맞는지는 모르겠습니다 ㅠㅠ 혹시 아시는 분 댓글 부탁드립니다!)
2. 행렬식(determinant) 구하기
보통 우리가 고등학교 때 배운 행렬식은 2x2 행렬에 대한 행렬식 (ad - bc) 밖에 없기 때문에
numpy에 내장되어있는 함수를 한 번 찾아보았더니 역시나! 하고 있었다.
바로 numpy.linalg.det(Mat) 함수인데, 행렬식을 구할 수 있는 행렬을 넣으면 바로
행렬식의 값을 리턴해준다.
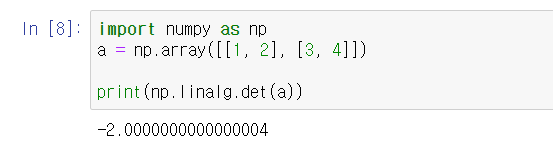
실수 값이 나오므로 꼭 소수점 처리를 해주도록 하자!
3. 단위행렬, 대각 행렬, 대각합 구하기
원래는 그만 쓰려했는데 이대로 끝나기 아쉬워서 몇 가지 더 정리하려 한다..
- np.eye(n) : n차 단위행렬(항등 행렬)을 반환해준다.
- np.diag(mat) : 인자로 받은 행렬에 대한 대각 행렬을 반환해준다.

이런 식으로 n차 행렬이 있으면 1*n 꼴로 반환해줍니다.
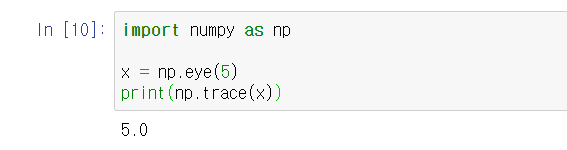
- np.trace(mat) : 대각선 원소들을 전부 더해줍니다. (= sum(diag))
'Artificial Intelligence' 카테고리의 다른 글
| [numpy] 5주차 eigen vector, value (0) | 2020.04.15 |
|---|---|
| [numpy] 5주차 PIL로 image 읽고 변환하기 (0) | 2020.04.15 |
| [numpy] 4주차 gram-schmidt, reflection matrix (2) | 2020.04.09 |
| [numpy] 2주차 기본 행렬 연산과 인덱싱 (1) | 2020.03.23 |
| [numpy] 1주차 numpy 기초 함수 및 행렬 변환 정리 (1) | 2020.03.19 |
저번 시간에는 행렬 간의 기본적인 연산과 인덱싱에 대해 알아보았었다.
따라서 이번에는 저번 시간에 배운 기본적인 연산을 이용해
행렬 변환과 행렬식을 구하는 방법에 대해 글을 써보려 한다.
1. vector를 가지고 행렬 transformation 하기
임의의 벡터 x를 가지고 어떤 행렬 A에 대해 transformation을 하는 방법은 간단하다.
단, 벡터와 행렬의 공간이 맞아야 한다. (벡터 공간의 수와 행렬의 행)
예시를 보자

3 x 3 행렬 A에 대해 (1,2,3)으로 정의된 vector x의 transformation을 나타내려면
행렬 A의 각 행에 대해서 vector를 내적 하면 된다.
하지만 좀 보기 불편해 보인다.
사실 transformation을 하는데에 따로 함수를 정의할 필요는 없다.

그냥 내적 해도 같은 결과가 나오기 때문이다.
이는 vector에서 행렬로 transformation을 하던,
행렬에서 행렬로 하던 똑같은 결과가 나올 것을 암시한다.
행렬 -> 행렬로 transform을 하면

이러한 결과가 나온다.
어라? 이게 무슨 소리지?
이건 내적이지 transform이 아니잖아요!
벡터 간의 내적을 풀어보자면
임의의 벡터 u, v가 있을 때 벡터 u와 v를 내적 한 것은
u를 transpose 시키고 벡터 v와 벡터 곱을 한 것과 같다.
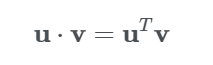
따라서 내적 = transform 이 되는 것이다.
(위키피디아에서 해석해본 결과 이런 것 같은데 저도 정확히 이게 맞는지는 모르겠습니다 ㅠㅠ 혹시 아시는 분 댓글 부탁드립니다!)
2. 행렬식(determinant) 구하기
보통 우리가 고등학교 때 배운 행렬식은 2x2 행렬에 대한 행렬식 (ad - bc) 밖에 없기 때문에
numpy에 내장되어있는 함수를 한 번 찾아보았더니 역시나! 하고 있었다.
바로 numpy.linalg.det(Mat) 함수인데, 행렬식을 구할 수 있는 행렬을 넣으면 바로
행렬식의 값을 리턴해준다.

실수 값이 나오므로 꼭 소수점 처리를 해주도록 하자!
3. 단위행렬, 대각 행렬, 대각합 구하기
원래는 그만 쓰려했는데 이대로 끝나기 아쉬워서 몇 가지 더 정리하려 한다..
- np.eye(n) : n차 단위행렬(항등 행렬)을 반환해준다.
- np.diag(mat) : 인자로 받은 행렬에 대한 대각 행렬을 반환해준다.

이런 식으로 n차 행렬이 있으면 1*n 꼴로 반환해줍니다.
- np.trace(mat) : 대각선 원소들을 전부 더해줍니다. (= sum(diag))

'Artificial Intelligence' 카테고리의 다른 글
| [numpy] 5주차 eigen vector, value (0) | 2020.04.15 |
|---|---|
| [numpy] 5주차 PIL로 image 읽고 변환하기 (0) | 2020.04.15 |
| [numpy] 4주차 gram-schmidt, reflection matrix (2) | 2020.04.09 |
| [numpy] 2주차 기본 행렬 연산과 인덱싱 (1) | 2020.03.23 |
| [numpy] 1주차 numpy 기초 함수 및 행렬 변환 정리 (1) | 2020.03.19 |
