병합 정렬
- 정의 : 분할 정복 알고리즘의 하나로 정렬되지 않은 리스트를 잘라 나누어 정렬 한 후 다시 병합하는 정렬기법이다.
-
작동 방식
- 1. 분할: 정렬 되지 않은 리스트를 절반으로 나누어 두 부분 리스트로 나눈다. 이를 눈에 보일만큼 작은 크기로 나누어 질 때까지 계속 실행한다
- 2. 정복: 나누어진 리스트들을 재귀적으로 다시 정렬한다.
- 3. 결합: 정렬된 리스트들을 하나의 배열에 병합한다.
작동 방식만 보고는 이해가 안되니 바로 그림으로 살펴 보도록 하자.
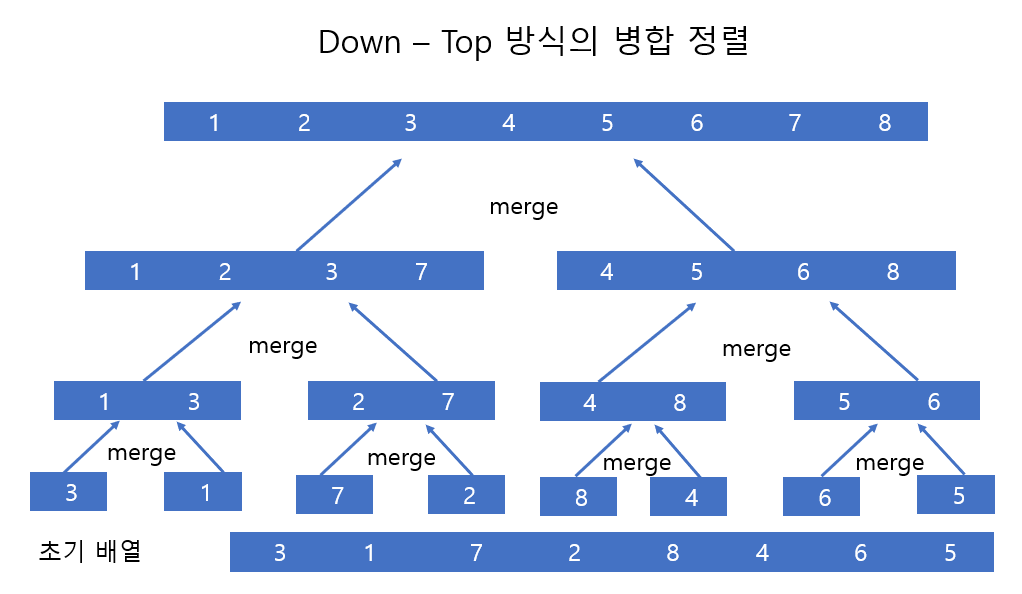
위 그림은 초기 배열 [3,1,7,2,8,4,6,5]를 밑에서 부터 위로 정렬하는 Down-Top 방식의 병합 정렬이다.
-
알고리즘의 진행
- 1. 전체 리스트의 앞의 반, 뒤의 반을 병합 정렬을 통해서 정렬
- 2. 병합 정렬에 의해서 앞의 반, 뒤의 반 모두 오름차순으로 정렬을 완료함(~분할 과정)
- 3. 두 리스트를 병합
- Python 3 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
def merge(A, B):
if (len(A) == 0):
return B
if (len(B) == 0):
return A
if(A[0] < B[0]):
return [A[0]] + merge(A[1:], B)
else:
return [B[0]] + merge(A,B[1:])
def mergeSort(arr):
if(len(arr) == 1):
return arr
return merge(mergeSort(arr[:int(len(arr)/2)]), mergeSort(arr[int(len(arr)/2):]))
initial_arr = [3,1,7,2,8,4,6,5]
print(mergeSort(initial_arr))
|
cs |
- 수업시간에 킹갓 교수님이 짜신 파이썬 코드만큼 쉽고 간단하게 짤 수가 없어서 어쩔 수 없이 파이썬 코드를 가져왔다.
mergeSort 함수는 리스트를 분할하고, merge 함수는 분할된 리스트를 정복,합병하는 역할을 하고있다.
- 시간복잡도 : 위 병합정렬 방식의 시간복잡도는 down - top 방식을 표현한 그림처럼 원소 하나를 가지는 리스트 ~ 모두 정렬된 하나의 리스트로 가는 과정이므로, 점화식으로 표현하면 T(n) = 2T(n/2) + 2 가 된다. 이 점화식은 nlogn의 시간복잡도를 갖는다. 또한 이는 어차피 원소 하나일때부터 쭉 올라가서 리스트가 뒤죽박죽이든, 말든 같은 시간 복잡도를 갖는다. 하지만 실제로 원소들이 자주 움직이는 방식이므로 퀵정렬 보다 시간이 많이 걸린다는 단점이있다.
퀵 정렬
우선 퀵정렬은 가장 널리 쓰이는 정렬 알고리즘이다. C++에서 sort 함수를 쓰면 퀵 정렬로 정렬된다
- 정의 : 이름부터 당당히 빠른 정렬이라고 지어져있다. 이 정렬의 핵심 아이디어는 특정 원소(pivot)을 중심으로 "작은 것"은 왼쪽, "큰것"은 오른쪽에 두는 방법이다.
-
작동 방식
- 보통 pivot이라고 칭하는 특정 원소는 처음에 배열의 첫 원소로 설정한다
- 이후 pivot 자리를 비우고, 배열의 끝에서 부터 원소를 비교하며, pivot 보다 원소가 크면 그대로, 작으면 빈 자리(기존에 pivot이 있던 자리)로 이동시킨다 - why? 오름차순이고, 오른쪽부터 비교하니까 크면 냅두고 작으면 옮긺
- pivot 보다 원소가 작은 다른 원소가 이동했으니 그 자리가 비어있다. 이 자리를 채우기 위해 다시 pivot은 왼쪽부터 탐색을 하며 이번엔 자기보다 원소가 큰 다른 원소를 찾아 빈 자리에 넣어준다.
- 이 과정을 빈자리 기준으로 왼쪽이 pivot보다 모두 작고, 오른쪽이 모두 클 때까지 반복한다(오른쪽,왼쪽,오른쪽,왼쪽...)
- 마지막 빈 자리에 pivot을 넣는다
- 이 과정을 계속 반복한다.
이것 또한 작동방식만 봐선 절대 이해가 안될것이다. (사실 말로 잘 설명 못하겠어요.. ㅠㅠ)
고렇다면 예제를 보자!
5 2 4 8 7 3 1 6 (pivot = 5)
_ 2 4 8 7 3 1 6 (6부터 거꾸로)
1 2 4 8 7 3 _ 6 (1부터)
1 2 4 _ 7 3 8 6
1 2 4 3 7 _ 8 6 (오른쪽에는 더이상 없음!)
1 2 4 3 7 _ 8 6
1 2 4 3 _ 7 8 6 (왼쪽도 더이상 없음!)
1 2 4 3 5 7 8 6 (pivot 집어넣고 끝!)
참고로 이 과정을 한 번만 하는 것이아니라 pivot 이었던 원소 기준으로 왼쪽,오른쪽 수들을 또 quick sort 하면서 이 과정을 왼쪽, 오른쪽 수가 1 또는 0이 될 때까지 반복한다.
보통 퀵 소트를 이용하는 이유는 이 pivot 때문에 한 바퀴를 돌때마다 반드시 적어도 1개의 원소가 자기 자리를 찾게되서 이후에 정렬할 개수가 줄어들기 때문에 보통의 O(nlogn) 정렬 알고리즘보다 훨씬 빠르게 동작한다.
- Python 3 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
def quickSort(arr):
if(len(arr) == 1) or (len(arr) == 0):
return arr
pivot = arr[0]
left = []
right = []
for x in arr[1:]:
if (x < pivot):
left.append(x)
else:
right.append(x)
return quickSort(left) + [pivot] + quickSort(right)
init_arr = [5,2,4,8,7,3,1,6]
print(quickSort(init_arr))
|
cs |
- 이 코드도 원래 c++로 짜서해야하는데 교수님 코드가 너무 쉽고 간단해서 가져왔다.
- 참고로 이 코드는 위의 예시대로 짠 코드는 아니구 left, right 배열을 만들어 처리하였습니다! (메모리 효율성 떨어짐)
코드 설명을 하자면 , 뒤죽박죽인 리스트를 quickSort 함수에 집어넣고, merge sort처럼 분할 정복 기법을 이용해 기준(pivot)보다 작은걸 left, 큰걸 right로 두고 계속 분할하고, 이후 정렬(return 문에서 작동)하는 과정이다.
-
시간복잡도
- 가장 좋을 때 : 기준의 왼쪽, 오른쪽에 같은 수의 원소가 이동하는 경우 ex) pivot = 1, arr = 12345678
- 점화식 : T(n) = 2T(n/2) + n = O(nlogn)
- 가장 나쁜 경우 : 기준의 왼쪽 또는 오른쪽 한 쪽으로만 원소가 쏠리는 경우 ex) pivot = 1, arr = 18765432
- 점화식 : T(n) = T(n-1) + n = O(n^2)
이렇게 오늘은 분할 정복 기법을 사용하는 두 정렬 방식인 병합 정렬과 퀵 정렬에 대해 살펴보았다.
이 정렬 방식들은 머리로 생각하기엔 앞서 설명한 버블 정렬과 삽입 정렬보다 어렵지만, 확실히 빠르기때문에
단지 머리 아프다고 시간복잡도가 높은 정렬을 쓰기 보단, 머리가 좀 빠지더라고 얼른 시간복잡도가 좋은 정렬에 익숙해져보자!
'학업 > algorithm class' 카테고리의 다른 글
| 이진 탐색 트리 (0) | 2019.10.21 |
|---|---|
| 힙 정렬(Heap sort) (0) | 2019.10.19 |
| [정렬] 버블 정렬과 삽입 정렬 (0) | 2019.10.17 |
| [Algorithm] 정렬 (0) | 2019.10.17 |
| 탐색 문제의 최적성과 점화식 (0) | 2019.10.16 |
