이진 탐색트리란?
이진 탐색트리는 다음과 같은 속성이 있는 자료 구조이다.
- 각 노드에 값이 있고, 각 노드마다 최대 두 개의 자식을 갖는다.
- 왼쪽 자식은 부모보다 키 값이 작고, 오른쪽 자식은 부모보다 키 값이 크다.
이진 탐색트리 예시
-
{8,3,10,1,6,14,4,7,13}
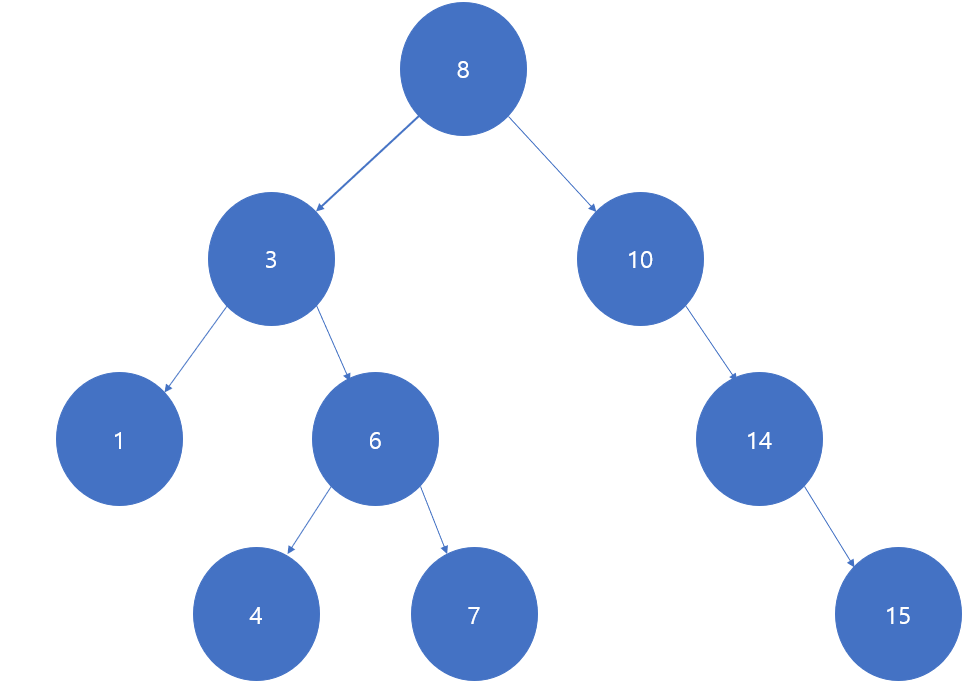
이 노드를 기준으로,
루트 8 의 왼쪽 서브트리는 3부터 그 이하의 노드들로 이루어진 트리이고,
루트 8 의 오른쪽 서브트리는 10부터 그 밑에있는 노드들로 이루어진 트리이다.
이진 탐색 트리는 유일하지 않다.
예를 들어 {1, 2, 3, 4}에 대한 이진 탐색 트리는
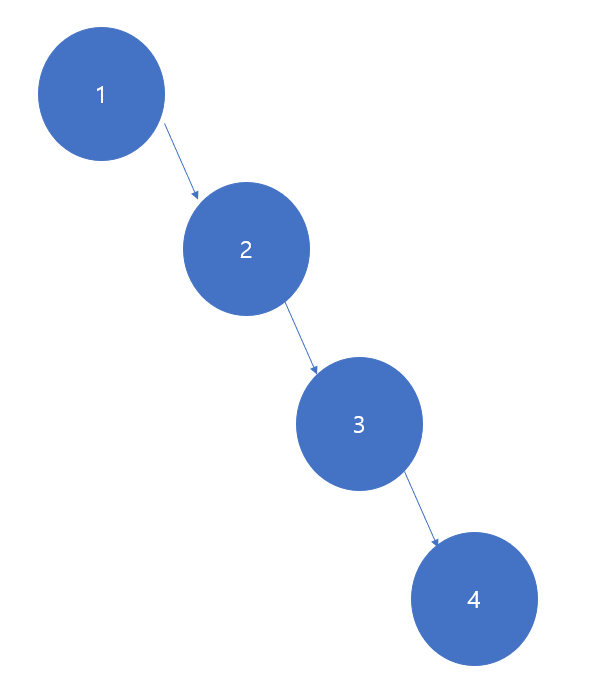
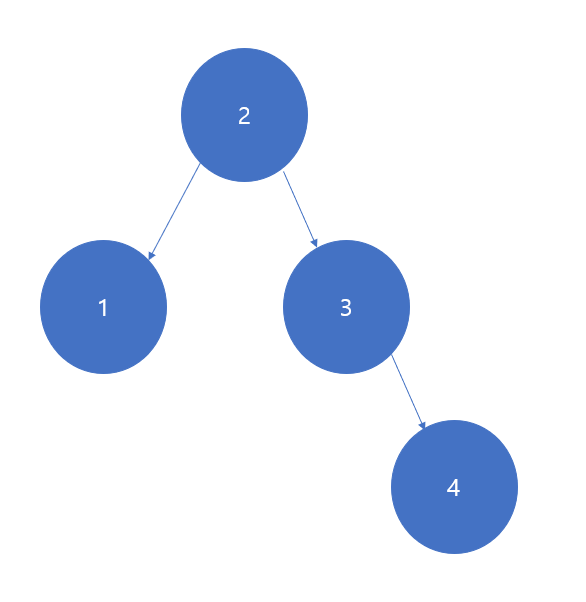
이런식으로 두가지 이상으로 표현 가능하다.
만약 어떤 키 값이 자주 접근될 지 모른다면, 균형잡힌 오른쪽 트리가 유리할 것이고,
만약 1 값이 가장 자주 접근된다면 균형이 잡히지 않은 것이 유리하다
-
C++ 이진 탐색 트리 구현
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
|
//알고리즘 이진 탐색 트리 탐색과 삽입 구현
#include <iostream>
#define null 0
using namespace std;
template <typename T>
class Tree;
template <typename T>
class Node {
friend class Tree<T>;
private:
T key;
Node* left;
Node* right;
Node* parent;
public:
Node(T key = 0, Node * left = null, Node * right = null, Node* parent = null) {
this->key = key;
this->left = left;
this->right = right;
this->parent = parent;
}
friend ostream& operator<<(ostream& os, const Node<T>& node) {
os << "[data]" << node.key << endl;
if (node.left != null) {
os << "[left]" << node.left->key << endl;
}
if (node.right != null) {
os << "[right]" << node.right->key << endl;
}
return os;
}
};
template <typename T>
class Tree {
private:
Node<T>* root;
public:
Tree(T key = 0) {
root = new Node<T>(key);
}
//Tree 만들기
void buildSearchTree() {
insertNode(new Node<int>(3));
insertNode(new Node<int>(10));
insertNode(new Node<int>(14));
insertNode(new Node<int>(2));
insertNode(new Node<int>(5));
insertNode(new Node<int>(11));
insertNode(new Node<int>(16));
}
void insertNode(Node<T>* node) {
//중복이 없을 떄
if (search(root, node->key) == null) {
Node<T>* parent = null;
Node<T>* current = root;
//작으면 왼쪽, 크면 오른쪽
//새 노드의 부모가 정해짐
while (current != null) {
parent = current;
if (node->key < parent->key) {
current = current->left;
}
else {
current = current->right;
}
}
if (node->key < parent->key) {
parent->left = node;
}
else {
parent->right = node;
}
cout << "Inserted" << node->key << endl;
}
}
Node<T>* getRoot() {
return root;
}
//전위순회
void preorder(Node<T>* current) {
if (current != null) {
visit(current);
preorder(current->left);
preorder(current->right);
}
}
void visit(Node<T>* current) {
cout << current->key << " ";
}
//탐색 연산
Node<T>* search(Node<T>* current, T key) {
if (current == null) return null;
if (key == current->key) {
return current;
}
else if (key < current->key) {
search(current->left, key);
}
else {
search(current->right, key);
}
}
};
int main()
{
Tree<int> tree(8);
tree.buildSearchTree();
//Tree 출력
cout << "preorder >>";
tree.preorder(tree.getRoot()); //루트 값 받아 그 값부터 전위순회
cout << "\n";
//tree에 값 넣어보기
tree.insertNode(new Node<int>(4));
cout << "Preorder >> ";
tree.preorder(tree.getRoot());
cout << "\n";
//tree 탐색
int number;
cout << "input number to search >>";
cin >> number;
Node<int>* found = tree.search(tree.getRoot(), number);
if (found != null) {
cout << "Fount node." << *found << "\n";
}
else {
cout << "Not found node." << "\n";
}
}
|
cs |
C++ 이진 탐색 트리 구현하기 (Binary Search Tree)
이진 탐색 트리 (Binary Search Tree) 이진 탐색트리는 데이터의 크기에 따라 노드의 위치가 다르다. 정의는 아래와 같다. (1) 모든 원소는 서로 다른 유일한 키를 갖는다.(2) 왼쪽 서브 트리에 있는 원소의 키는 그 루트의 키보다 작다.(3) 오른쪽 서브 트리에 있는 원소의 키는 그 루트의 키보다 크다.(4) 왼쪽 서브트리와 오른쪽 서브트리도 이진 탐색 트리이다. 이진 탐색 트리 C++ 구현 이제 이진 탐색트리를 구현할텐데, 탐색(sear
lx5475.github.io
이 코드는 여기서 참고하였습니다.
-
이진 탐색 트리 검색
- 이진 탐색 트리에 원하는 값 k가 들어 있는가?
1. 트리가 비어있다면 k는 트리에 있을 수 없다.
2. 만약 루트의 값이 원하는 값 k라면, 이 값을 리턴한다.
3. 만약 루트의 값이 k보다 크다면 (k가 루트보다 작으면) k는 루트의 왼쪽 서브 트리에 있어야하며,
만약 루트의 값이 k보다 작다면 (k가 루트보다 크다면) k는 루트의 오른쪽 서브 트리에 있어야한다.
4. 2~3의 과정을 반복
-
이진 탐색 트리 삭제
- 삭제할 노드가 무엇인가에 따라서 세 가지 경우가 존재한다
1. 노드가 리프이다
-> 그냥 지우자
2. 노드가 하나의 자식을 가진다
-> 노드를 지우고, 자식을 원래 노드의 위치로 옮긴다
3. 노드가 두 자식을 가진다
case1 : 서브 트리의 원소들을 모두 모아 다시 트리를 만든다
case2 : 트리의 모양을 최대한 유지하는 방법. 삭제할 노드의 키 값에서 바로 앞이나 바로 뒤에 있는 노드를 찾고, 이 노드를 원래 노드의 위치로 옮긴 후 다시 옮긴 노드 자리를 두고 1~3 번 과정을 거치는 경우
삭제의 예
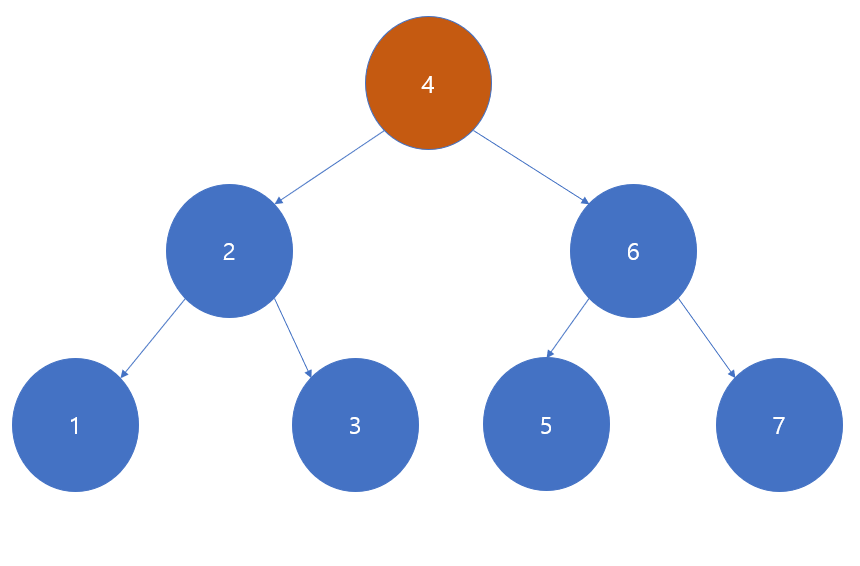
루트 4를 삭제한 경우
바로 앞 값 5을 올린다.
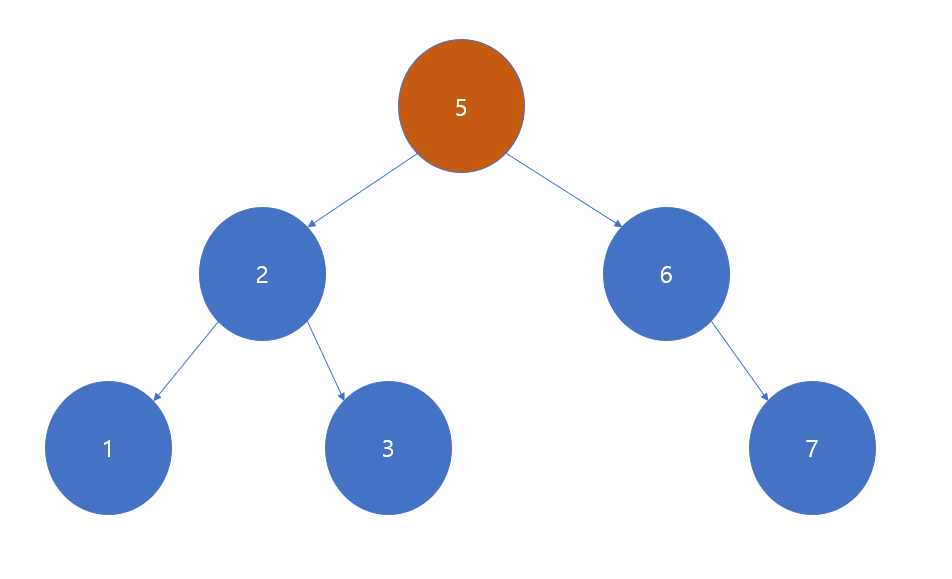
5는 리프이기 때문에 5자리를 지우고 루트자리에 5를 집어넣기만하면 된다.
'algorithm class' 카테고리의 다른 글
| 위상 정렬 (0) | 2020.02.12 |
|---|---|
| 유니온 파인드(Disjoint-set) 이란? (0) | 2020.01.06 |
| 힙 정렬(Heap sort) (0) | 2019.10.19 |
| 분할 정복 기법 (병합 정렬, 퀵 정렬) (0) | 2019.10.18 |
| [정렬] 버블 정렬과 삽입 정렬 (0) | 2019.10.17 |
이진 탐색트리란?
이진 탐색트리는 다음과 같은 속성이 있는 자료 구조이다.
- 각 노드에 값이 있고, 각 노드마다 최대 두 개의 자식을 갖는다.
- 왼쪽 자식은 부모보다 키 값이 작고, 오른쪽 자식은 부모보다 키 값이 크다.
이진 탐색트리 예시
-
{8,3,10,1,6,14,4,7,13}

이 노드를 기준으로,
루트 8 의 왼쪽 서브트리는 3부터 그 이하의 노드들로 이루어진 트리이고,
루트 8 의 오른쪽 서브트리는 10부터 그 밑에있는 노드들로 이루어진 트리이다.
이진 탐색 트리는 유일하지 않다.
예를 들어 {1, 2, 3, 4}에 대한 이진 탐색 트리는


이런식으로 두가지 이상으로 표현 가능하다.
만약 어떤 키 값이 자주 접근될 지 모른다면, 균형잡힌 오른쪽 트리가 유리할 것이고,
만약 1 값이 가장 자주 접근된다면 균형이 잡히지 않은 것이 유리하다
-
C++ 이진 탐색 트리 구현
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
|
//알고리즘 이진 탐색 트리 탐색과 삽입 구현
#include <iostream>
#define null 0
using namespace std;
template <typename T>
class Tree;
template <typename T>
class Node {
friend class Tree<T>;
private:
T key;
Node* left;
Node* right;
Node* parent;
public:
Node(T key = 0, Node * left = null, Node * right = null, Node* parent = null) {
this->key = key;
this->left = left;
this->right = right;
this->parent = parent;
}
friend ostream& operator<<(ostream& os, const Node<T>& node) {
os << "[data]" << node.key << endl;
if (node.left != null) {
os << "[left]" << node.left->key << endl;
}
if (node.right != null) {
os << "[right]" << node.right->key << endl;
}
return os;
}
};
template <typename T>
class Tree {
private:
Node<T>* root;
public:
Tree(T key = 0) {
root = new Node<T>(key);
}
//Tree 만들기
void buildSearchTree() {
insertNode(new Node<int>(3));
insertNode(new Node<int>(10));
insertNode(new Node<int>(14));
insertNode(new Node<int>(2));
insertNode(new Node<int>(5));
insertNode(new Node<int>(11));
insertNode(new Node<int>(16));
}
void insertNode(Node<T>* node) {
//중복이 없을 떄
if (search(root, node->key) == null) {
Node<T>* parent = null;
Node<T>* current = root;
//작으면 왼쪽, 크면 오른쪽
//새 노드의 부모가 정해짐
while (current != null) {
parent = current;
if (node->key < parent->key) {
current = current->left;
}
else {
current = current->right;
}
}
if (node->key < parent->key) {
parent->left = node;
}
else {
parent->right = node;
}
cout << "Inserted" << node->key << endl;
}
}
Node<T>* getRoot() {
return root;
}
//전위순회
void preorder(Node<T>* current) {
if (current != null) {
visit(current);
preorder(current->left);
preorder(current->right);
}
}
void visit(Node<T>* current) {
cout << current->key << " ";
}
//탐색 연산
Node<T>* search(Node<T>* current, T key) {
if (current == null) return null;
if (key == current->key) {
return current;
}
else if (key < current->key) {
search(current->left, key);
}
else {
search(current->right, key);
}
}
};
int main()
{
Tree<int> tree(8);
tree.buildSearchTree();
//Tree 출력
cout << "preorder >>";
tree.preorder(tree.getRoot()); //루트 값 받아 그 값부터 전위순회
cout << "\n";
//tree에 값 넣어보기
tree.insertNode(new Node<int>(4));
cout << "Preorder >> ";
tree.preorder(tree.getRoot());
cout << "\n";
//tree 탐색
int number;
cout << "input number to search >>";
cin >> number;
Node<int>* found = tree.search(tree.getRoot(), number);
if (found != null) {
cout << "Fount node." << *found << "\n";
}
else {
cout << "Not found node." << "\n";
}
}
|
cs |
C++ 이진 탐색 트리 구현하기 (Binary Search Tree)
이진 탐색 트리 (Binary Search Tree) 이진 탐색트리는 데이터의 크기에 따라 노드의 위치가 다르다. 정의는 아래와 같다. (1) 모든 원소는 서로 다른 유일한 키를 갖는다.(2) 왼쪽 서브 트리에 있는 원소의 키는 그 루트의 키보다 작다.(3) 오른쪽 서브 트리에 있는 원소의 키는 그 루트의 키보다 크다.(4) 왼쪽 서브트리와 오른쪽 서브트리도 이진 탐색 트리이다. 이진 탐색 트리 C++ 구현 이제 이진 탐색트리를 구현할텐데, 탐색(sear
lx5475.github.io
이 코드는 여기서 참고하였습니다.
-
이진 탐색 트리 검색
- 이진 탐색 트리에 원하는 값 k가 들어 있는가?
1. 트리가 비어있다면 k는 트리에 있을 수 없다.
2. 만약 루트의 값이 원하는 값 k라면, 이 값을 리턴한다.
3. 만약 루트의 값이 k보다 크다면 (k가 루트보다 작으면) k는 루트의 왼쪽 서브 트리에 있어야하며,
만약 루트의 값이 k보다 작다면 (k가 루트보다 크다면) k는 루트의 오른쪽 서브 트리에 있어야한다.
4. 2~3의 과정을 반복
-
이진 탐색 트리 삭제
- 삭제할 노드가 무엇인가에 따라서 세 가지 경우가 존재한다
1. 노드가 리프이다
-> 그냥 지우자
2. 노드가 하나의 자식을 가진다
-> 노드를 지우고, 자식을 원래 노드의 위치로 옮긴다
3. 노드가 두 자식을 가진다
case1 : 서브 트리의 원소들을 모두 모아 다시 트리를 만든다
case2 : 트리의 모양을 최대한 유지하는 방법. 삭제할 노드의 키 값에서 바로 앞이나 바로 뒤에 있는 노드를 찾고, 이 노드를 원래 노드의 위치로 옮긴 후 다시 옮긴 노드 자리를 두고 1~3 번 과정을 거치는 경우
삭제의 예

루트 4를 삭제한 경우
바로 앞 값 5을 올린다.

5는 리프이기 때문에 5자리를 지우고 루트자리에 5를 집어넣기만하면 된다.
'algorithm class' 카테고리의 다른 글
| 위상 정렬 (0) | 2020.02.12 |
|---|---|
| 유니온 파인드(Disjoint-set) 이란? (0) | 2020.01.06 |
| 힙 정렬(Heap sort) (0) | 2019.10.19 |
| 분할 정복 기법 (병합 정렬, 퀵 정렬) (0) | 2019.10.18 |
| [정렬] 버블 정렬과 삽입 정렬 (0) | 2019.10.17 |
