유니온 파인드(Union Find)란? 서로소 집합 자료구조(Disjoint-set)이라는 알고리즘으로도 불리며, 서로 다른 부분집합 간의 병합(Union) 과정을 의미한다.
유니온 파인드는 서로 다른 집합을 합치거나, 한 집합이 다른 집합에 속해있는지를 확인하는 연산 두 가지로 이루어져있는데, 전자를 Union 이라하며, 후자를 Find라고 한다. 참고로 유니온 파인드는 집합이지만 트리로 생각하여 푸는 건데, 아래에서 설명하겠다.
1. 초기화 : 유니온 파인드는 우선 처음에 자기 자신을 루트라고 정하고 시작한다.
|
1
2
3
|
for (int i = 0; i <= n; i++) {
p[i] = i;
}
|
cs |
2. Union : Union(x,y)는 y가 속한 집합을 x가 속한 집합에 포함시키는 함수이다.

위 그림은 {1},{2},{3},{4},{5}를 표현한 그림이다. 각 집합은 어떠한 상관관계도 보이지 않는다.
1) Union(1,2)
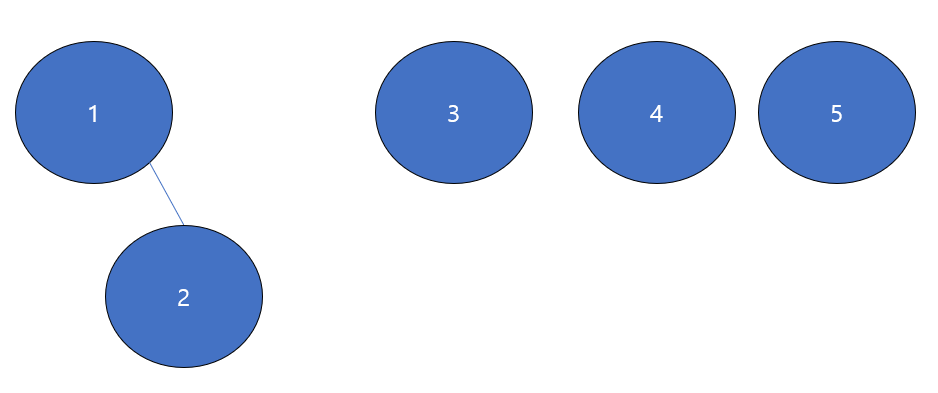
2를 1에 포함시켰더니 위 그림과 같이 2가 1 밑에 붙는것을 알 수 있다.
이때 2의 루트는 1이 된다.(Parent[2] = 1)
2)Union(3,4)
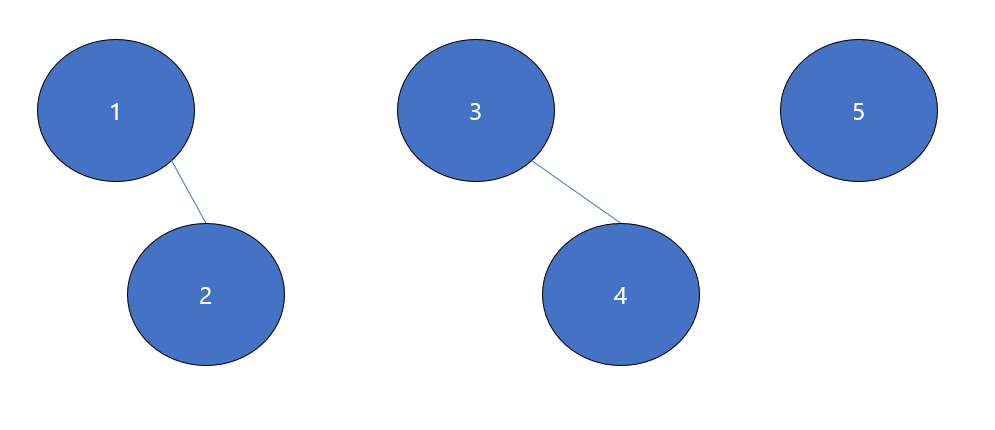
Union(1,2)의 과정과 동일하다.(Parent[4] = 3)
3)Union(4,5)
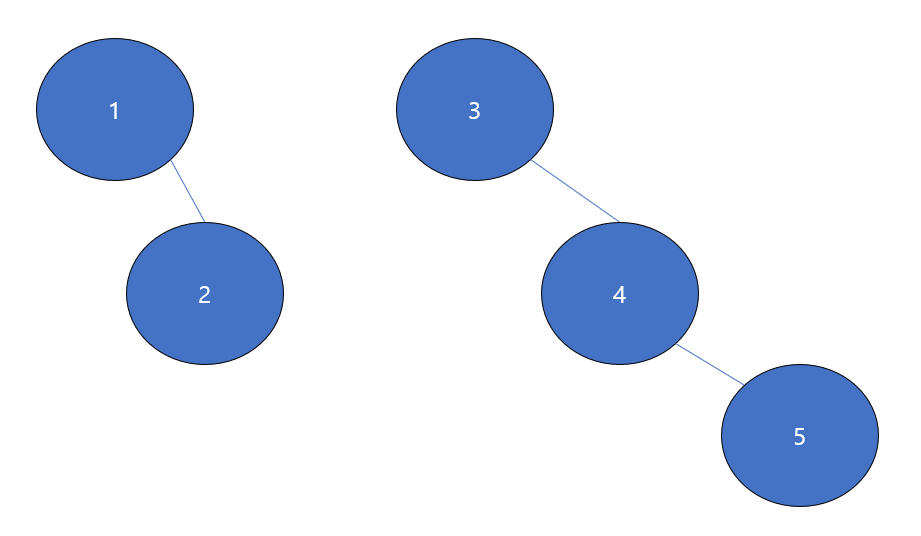
위와 동일하게 붙는다. -> 현재 부분집합 = {1,2}, {3,4,5}
그렇다면 2개 이상의 부분집합끼리도 붙일 수 있을까?
4)Union(2,5)
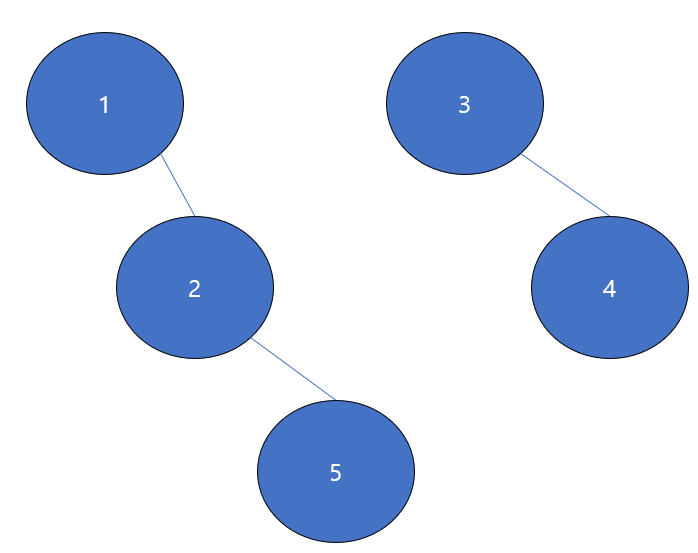
어라? 분명 {3,4,5}를 {1,2}로 붙였는데 "5"만 움직여 붙어버리는 것을 볼 수 있다!(Parent[5] = 2)
이런 경우를 방지하기 위해 Find 함수를 사용한다.
3. Find : Find는 그 루트가 무엇인지? 찾는 함수이다.
루트는 부모노드들의 부모노드, 즉 맨 위 노드를 말하기 때문에 재귀함수 호출을 이용하여 구현 가능하다.
|
1
2
3
4
5
6
7
|
int find(int x){
if(Parent[x] == x) return x;
return find(Parent[x]);
}
|
cs |
그렇다면 Find를 이용하여 다시 Union으로 넘어가보자.

아까 이 상황에서 똑같이 Union(2,5)를 시도해보자.
find(5)를 하면 5의 루트 3이 반환되고, find(2)를 하면 2의 루트 1이 반환된다.
Union은 사실 루트끼리 붙여버리는 것이다.
따라서,
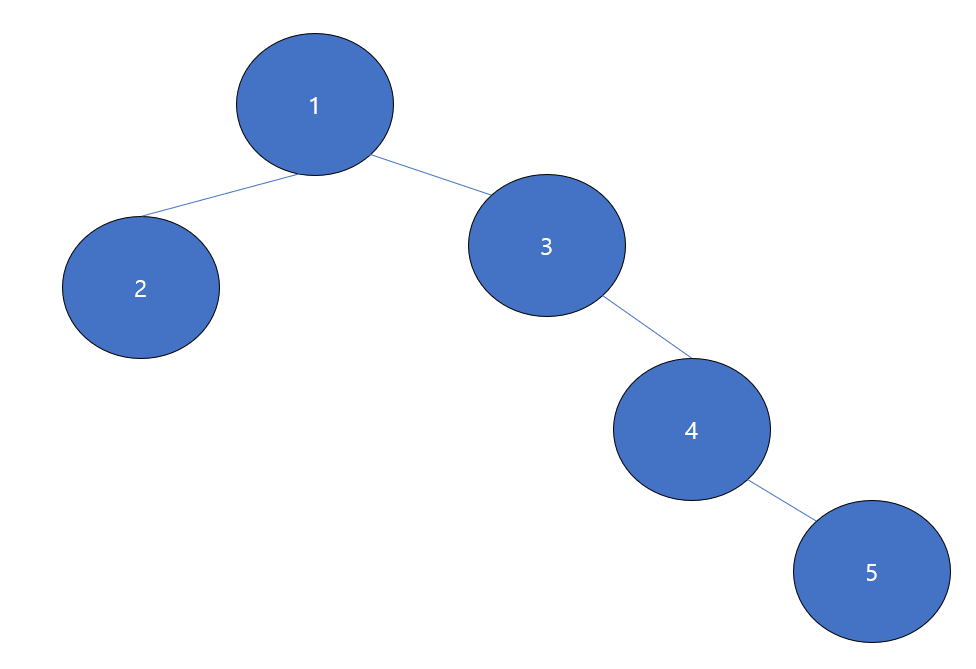
이렇게 같은 집합이 되는 것을 확인할 수 있다.
이 과정을 다시 코드로 보면,
|
1
2
3
4
5
6
7
8
9
10
|
int find(int x) { //루트 찾기
if (p[x] == x) return x;
return p[x] = find(p[x]);
}
void uni(int x, int y) {
x = find(x);
y = find(y);
p[y] = x;
}
|
cs |
이렇게 되는데 사실 이것도 문제점이 하나 있다.
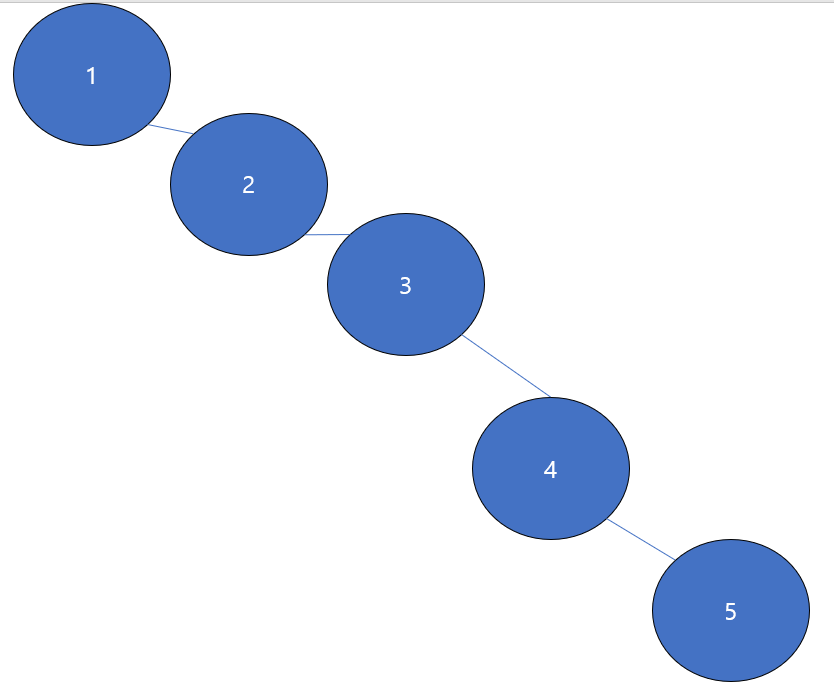
바로 이렇게 줄줄이 소시지 모양으로 트리가 형성될 수 있는데, 다른 집합이랑 붙일 때 5를 붙이게 되면 n번만큼의 find를 해야하기 때문에 시간복잡도가 O(N)으로 증가하게 된다. 따라서,
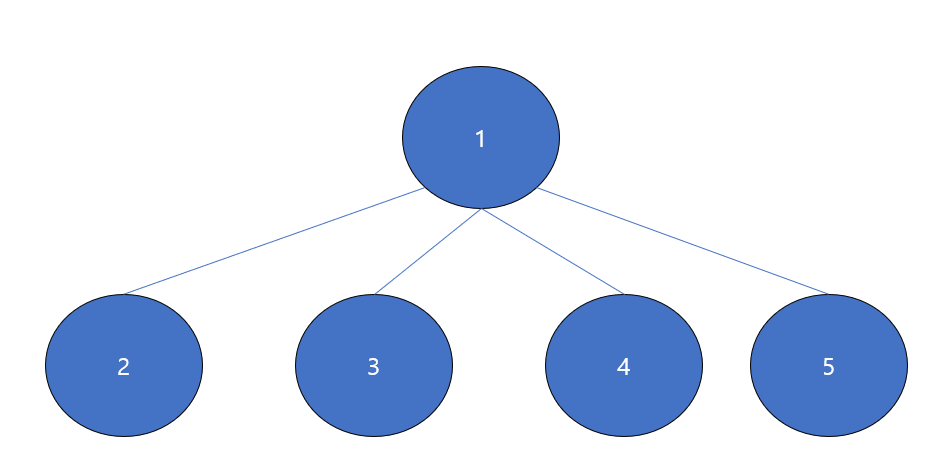
이런식으로 붙이는 게 중요한데, 이는 Find 함수 내에서 루트를 계속 바꿔가면서 구현 가능하다.
|
1
2
3
4
|
int find(int x) { //루트 찾기
if (p[x] == x) return x;
return p[x] = find(p[x]);
}
|
cs |
이런식으로 반환 시 p[X]를 주기적으로 부모의 P값과 바꿔주면,
같은 부분 집합에 속한 원소들의 P[X]값은 모두 동일하게 되며, find 시 한번에 끝낼 수 있다. --> O(1)
따라서 유니온 파인드 알고리즘의 시간복잡도는
- find : O(1)
- Union : O(N)
이며, 서로 같은 부분집합인지 확인하는 부분도 find로 해결가능하므로 O(1)에 풀 수 있다.
'학업 > algorithm class' 카테고리의 다른 글
| LCS 알고리즘 (0) | 2020.02.12 |
|---|---|
| 위상 정렬 (0) | 2020.02.12 |
| 이진 탐색 트리 (0) | 2019.10.21 |
| 힙 정렬(Heap sort) (0) | 2019.10.19 |
| 분할 정복 기법 (병합 정렬, 퀵 정렬) (0) | 2019.10.18 |
