하노이 탑이란?
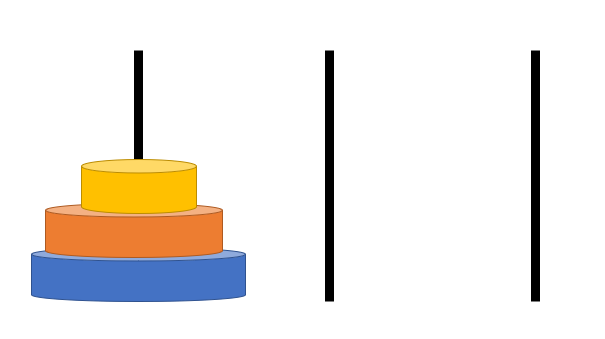
그림과 같이 세 개의 기둥과 이 기둥에 꽃을 수 있는 다양한 원판들이 있다.
이 탑은 두 가지 조건을 만족시키면서, 한 기둥에 꽂힌 원판들을 기존에 있던 그대로 다른 기둥으로 옮겨서 다시 쌓아야한다. 조건은 다음과 같다
1. 한 번에 하나의 원판만 옮길 수 있다.
2. 큰 원판이 작은 원판 위에 있어서는 안 된다.
이 문제는 원판의 개수가 적을 경우는 머리로 쉽게 생각할 수 있지만 조금만 커져도 원판을 이동시키는 횟수가 급격하게 많아기지 때문에 생각만큼 쉽지 않다.
이 문제에 대한 해결방안은 알고리즘 설계 기법중 하나인 재귀(recursion)을 이용하는 것인데 방법은 다음과 같다.
n=1 : 원판을 그냥 옮긴다
n=k 일 때 옮길 수 있다고 가정 한 후
n=k+1 일 때 (미리 가정한)위 방법을 이용하여 k개의 원판들을 기둥 2로 옮긴 후 k+1 번째 원판을 기둥 3으로 옮긴다.
이후 k개의 원반을 다시 기둥 3으로 옮긴다.
따라서 이 문제는 k개의 원반이 있을 때 원반의 이동 횟수를 T(k)라 하면
T(k) = T(k-1) + 1 + T(k-1) = 2T(k-1) + 1 이기 때문에
T(k) = 2^k - 1 이 됨을 알 수 있다.
이 문제의 재귀성을 이용하여 코드로 구현하면
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
#include <iostream>
using namespace std;
int hanoi(int n) { //하노이 탑 규칙에 따라 n개의 원반을 옮기는 횟수
if (n == 1) return 1;
return hanoi(n - 1) * 2 + 1;
}
int main()
{
int n; cin >> n;
cout << hanoi(n) << "\n";
return 0;
}
|
cs |
이런 식으로 구현 가능한데 사실 위에 있는 T(k) = 2^k - 1을 그대로 대입해도 답은 구할 수 있다.
Stable Marriage
문제: n명의 남자와 n명의 여자가 있을 때, 다음 조건을 만족하게 모든 남자와 여자를 1:1로 짝지울 수 있는가??
조건 - 1. 모든 남자와 여자는 이성에 대해 1등부터 n등까지 선호도가 있다.
2. (남자, 여자)의 쌍이 (a,b), (c,d)로 있는데, b가 a보다 c, c가 d보다 b를 더 좋아한다면 이들은 쌍을 깨고 새로운 쌍을 만들 게 된다. 이러한 일이 생기지 않게 쌍을 정하고 싶다.
이 설명을 그림으로 보면 다음과 같다
- 남녀 선호도
| A | WYXZ | W | BACD |
| B | YZWX | X | DABC |
| C | ZXYW | Y | ACBD |
| D | YXWZ | Z | BCAD |
여성의 기준으로 자신이 가장 선호하는 남성과 짝을 짓는다고 가정하자.
그렇다면 (B,W), (D,X),(A,Y)가 짝이 된 후 Z에서 충돌이 발생한다.
Z는 B를 가장 좋아하는데 B는 W보다 Z를 더 좋아한다. 따라서 다시 (B,Z)쌍이 구축되고 W는 B에게 버림받는다.
버림받은 W도 다시 짝을 찾기위해 이상형 리스트를 탐색해보는데, B는 이미 자신을 버렸기 때문에 안되고, A는 Y보다 자신을 더 좋아하기 때문에 다시 눈이 맞다 (A,W) 짝이 만들어진다.
이러면 또 Y가 버려지기 때문에 Y의 이상형 리스트를 다시 탐색하는데, C는 아직 짝이 없기 때문에 (C,Y)짝이 만들어져 모두 평화롭게(?) 짝을 지었다.
그렇다면 남성의 기준으로 봤을 땐 어떨까?
(A,W), (B,Y), (C,Z)가 짝이 된 후 D에서 충돌이 발생한다.
자신이 가장 좋아하는 Y는 이미 짝이 된 B를 더 좋아하기 때문에 안되고, X가 짝이 없기 때문에 (D,X) 짝이 만들어져 모두 짝을 지을 수 있게 되었다.
이처럼 Stable Marriage의 짝의 답은 하나가 아니다. 여러 경우의 완성된 짝이 만들어질 수 있다.
이 문제는 반드시 답을 도출할 수 있다(완성된 짝을 만들 수 있다)
왜냐하면 알고리즘 수행 과정에서 파트너가 바뀔 때마다 파트너의 선호도가 감소하고, 이상형 리스트엔 모든 이성이 담겨있기 때문에 어떻게든 만들어진다.
이를 시간복잡도로 표현하자면,
한 명의 관점에서 파트너가 바뀔 수 있는 횟수는 n번이며 위의 방법처럼 한 쪽이(남성 or 여성)이 계속 파트너를 찾는다면 n번 수행되므로 시간 복잡도는 O(n^2) 이다. 이는 가장 최악의 경우 (처음에 설정한 짝의 상대가 전부다 서로를 좋아하지않을 때)이고, 가장 최선은 O(n) 만에 알고리즘이 끝날 수도 있다.
'algorithm class' 카테고리의 다른 글
| 힙 정렬(Heap sort) (0) | 2019.10.19 |
|---|---|
| 분할 정복 기법 (병합 정렬, 퀵 정렬) (0) | 2019.10.18 |
| [정렬] 버블 정렬과 삽입 정렬 (0) | 2019.10.17 |
| [Algorithm] 정렬 (0) | 2019.10.17 |
| 탐색 문제의 최적성과 점화식 (0) | 2019.10.16 |
하노이 탑이란?

그림과 같이 세 개의 기둥과 이 기둥에 꽃을 수 있는 다양한 원판들이 있다.
이 탑은 두 가지 조건을 만족시키면서, 한 기둥에 꽂힌 원판들을 기존에 있던 그대로 다른 기둥으로 옮겨서 다시 쌓아야한다. 조건은 다음과 같다
1. 한 번에 하나의 원판만 옮길 수 있다.
2. 큰 원판이 작은 원판 위에 있어서는 안 된다.
이 문제는 원판의 개수가 적을 경우는 머리로 쉽게 생각할 수 있지만 조금만 커져도 원판을 이동시키는 횟수가 급격하게 많아기지 때문에 생각만큼 쉽지 않다.
이 문제에 대한 해결방안은 알고리즘 설계 기법중 하나인 재귀(recursion)을 이용하는 것인데 방법은 다음과 같다.
n=1 : 원판을 그냥 옮긴다
n=k 일 때 옮길 수 있다고 가정 한 후
n=k+1 일 때 (미리 가정한)위 방법을 이용하여 k개의 원판들을 기둥 2로 옮긴 후 k+1 번째 원판을 기둥 3으로 옮긴다.
이후 k개의 원반을 다시 기둥 3으로 옮긴다.
따라서 이 문제는 k개의 원반이 있을 때 원반의 이동 횟수를 T(k)라 하면
T(k) = T(k-1) + 1 + T(k-1) = 2T(k-1) + 1 이기 때문에
T(k) = 2^k - 1 이 됨을 알 수 있다.
이 문제의 재귀성을 이용하여 코드로 구현하면
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
#include <iostream>
using namespace std;
int hanoi(int n) { //하노이 탑 규칙에 따라 n개의 원반을 옮기는 횟수
if (n == 1) return 1;
return hanoi(n - 1) * 2 + 1;
}
int main()
{
int n; cin >> n;
cout << hanoi(n) << "\n";
return 0;
}
|
cs |
이런 식으로 구현 가능한데 사실 위에 있는 T(k) = 2^k - 1을 그대로 대입해도 답은 구할 수 있다.
Stable Marriage
문제: n명의 남자와 n명의 여자가 있을 때, 다음 조건을 만족하게 모든 남자와 여자를 1:1로 짝지울 수 있는가??
조건 - 1. 모든 남자와 여자는 이성에 대해 1등부터 n등까지 선호도가 있다.
2. (남자, 여자)의 쌍이 (a,b), (c,d)로 있는데, b가 a보다 c, c가 d보다 b를 더 좋아한다면 이들은 쌍을 깨고 새로운 쌍을 만들 게 된다. 이러한 일이 생기지 않게 쌍을 정하고 싶다.
이 설명을 그림으로 보면 다음과 같다
- 남녀 선호도
| A | WYXZ | W | BACD |
| B | YZWX | X | DABC |
| C | ZXYW | Y | ACBD |
| D | YXWZ | Z | BCAD |
여성의 기준으로 자신이 가장 선호하는 남성과 짝을 짓는다고 가정하자.
그렇다면 (B,W), (D,X),(A,Y)가 짝이 된 후 Z에서 충돌이 발생한다.
Z는 B를 가장 좋아하는데 B는 W보다 Z를 더 좋아한다. 따라서 다시 (B,Z)쌍이 구축되고 W는 B에게 버림받는다.
버림받은 W도 다시 짝을 찾기위해 이상형 리스트를 탐색해보는데, B는 이미 자신을 버렸기 때문에 안되고, A는 Y보다 자신을 더 좋아하기 때문에 다시 눈이 맞다 (A,W) 짝이 만들어진다.
이러면 또 Y가 버려지기 때문에 Y의 이상형 리스트를 다시 탐색하는데, C는 아직 짝이 없기 때문에 (C,Y)짝이 만들어져 모두 평화롭게(?) 짝을 지었다.
그렇다면 남성의 기준으로 봤을 땐 어떨까?
(A,W), (B,Y), (C,Z)가 짝이 된 후 D에서 충돌이 발생한다.
자신이 가장 좋아하는 Y는 이미 짝이 된 B를 더 좋아하기 때문에 안되고, X가 짝이 없기 때문에 (D,X) 짝이 만들어져 모두 짝을 지을 수 있게 되었다.
이처럼 Stable Marriage의 짝의 답은 하나가 아니다. 여러 경우의 완성된 짝이 만들어질 수 있다.
이 문제는 반드시 답을 도출할 수 있다(완성된 짝을 만들 수 있다)
왜냐하면 알고리즘 수행 과정에서 파트너가 바뀔 때마다 파트너의 선호도가 감소하고, 이상형 리스트엔 모든 이성이 담겨있기 때문에 어떻게든 만들어진다.
이를 시간복잡도로 표현하자면,
한 명의 관점에서 파트너가 바뀔 수 있는 횟수는 n번이며 위의 방법처럼 한 쪽이(남성 or 여성)이 계속 파트너를 찾는다면 n번 수행되므로 시간 복잡도는 O(n^2) 이다. 이는 가장 최악의 경우 (처음에 설정한 짝의 상대가 전부다 서로를 좋아하지않을 때)이고, 가장 최선은 O(n) 만에 알고리즘이 끝날 수도 있다.
'algorithm class' 카테고리의 다른 글
| 힙 정렬(Heap sort) (0) | 2019.10.19 |
|---|---|
| 분할 정복 기법 (병합 정렬, 퀵 정렬) (0) | 2019.10.18 |
| [정렬] 버블 정렬과 삽입 정렬 (0) | 2019.10.17 |
| [Algorithm] 정렬 (0) | 2019.10.17 |
| 탐색 문제의 최적성과 점화식 (0) | 2019.10.16 |
