문제
S는 다음과 같이 정의된다.
- S(0, n) = n (모든 양의 정수 n)
- S(k, n) = S(k-1, 1) + S(k-1, 2) + ... + S(k-1, n) (모든 양의 정수 k, n)
k와 n이 주어졌을 때, S(k, n)을 1,000,000,007로 나눈 나머지를 구하는 프로그램을 작성하시오.
풀이
이 문제같은 경우 어떤 성질을 이용해 점화식을 도출하고 ... 라는 일련의 과정보단, 직접 써보는 것이 이해가 빠를 것이다.
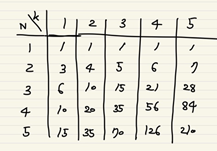
직접 써보니 이런 식의 표가 나왔다.
실제로 문제의 수식대로 저기까지만 계산해도 상당히 머리아픈데, 사람은 귀찮은걸 싫어하다보니.. 저거 쓰는 과정에서도 수를 빨리 도출해내는 법을 찾게 된다. 쓰다 보면 금방 찾는 규칙인데, 규칙은 다음과 같다.
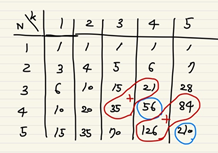
파란색 원 안의 수는 그 수 기준 왼쪽과 위쪽 빨간색 수의 합으로 나타낼 수 있다는 점이다.
이 부분은 생각해보면 간단한데, A[n][k] = A[n][k-1] + A[n-1][k-1] + ... + A[1][k-1] 이라는 속성을 표에 표시해보면
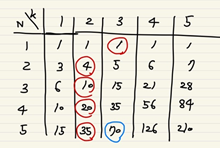
이런 식으로 나타낼 수 있고, 마지막 1은 n이 1일 때 모두 동일하므로 바꿔줄 수 있다.
즉, A[n][k] = A[n][k-1] + A[n-1][k]
그런데 이와 같은 경우, 문제에서 나오는 n이 최대 10억이므로 도저히 계산할 수 없는 지경에 이를 수 있다.
하지만 우리는 위에서 해당 유형을 몇 가지 풀어봤고, 문제 조건에서 주어지는 어떤 수의 제한이 50이라면?
좀 느낌이 다르게 느껴진다. 50 x 50 행렬은 충분히 이 유형에 쓰일 수 있기 때문이다.
따라서 저 공식을 k에 맞춰 다시 고쳐볼 수 있다. (불편하면 자세를 고쳐 앉으세요..!)
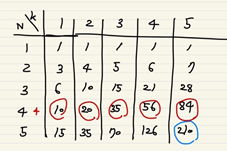
이렇게 가로로 눕혀놓는다면, n이 아무리 크더라도, k제한은 50이기 때문에 식이 확 줄어들게 된다.
이제 행렬로 표현해볼 건데, 이해를 돕기 위해 몇 가지 식만 적어본다.
- (3, 0) = (2, 0) + 1
- (3, 1) = (2, 1) + (2, 0) + 1
- (3, 2) = (2, 2) + (2, 1) + (2, 0) + 1
- (4, 2) = (3, 2) + (3, 1) + (3, 0) + 1
- (n, k) = (n-1, k) + ... + (n-1, 0) + 1
행렬로 나타내면 다음과 같다.

마지막으로 우리가 아는 행렬 거듭제곱으로 시각화한다면 다음과 같다.

소스 코드(.cpp)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll ans[55][55];
ll arr[55][55];
int k, n;
const int MOD = 1000000007;
void mul(ll A[55][55], ll B[55][55]) {
ll ret[55][55] = { 0, };
for (int i = 0; i < k+2; i++) {
for (int j = 0; j < k+2; j++) {
for (int a = 0; a < k+2; a++) {
ret[i][j] = (ret[i][j] + (A[i][a] * B[a][j])) % MOD;
}
}
}
for (int i = 0; i < 55; i++) {
for (int j = 0; j < 55; j++) {
A[i][j] = ret[i][j];
}
}
}
int main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> k >> n;
for (int i = 0; i < k + 2; i++) ans[i][i] = 1;
for (int i = 0; i < k + 2; i++) {
for (int j = 0; j <= i; j++) {
arr[i][j] = 1;
}
}
n--;
while (n > 0) {
if (n % 2 == 1) mul(ans, arr);
mul(arr, arr);
n /= 2;
}
ll sum = 0;
for (int i = 0; i < k + 2; i++) {
sum = (sum + ans[k + 1][i]) % MOD;
}
cout << sum << "\n";
return 0;
}'백준 문제풀이' 카테고리의 다른 글
| 백준 20173번 Imprecise Computer (1) | 2021.07.08 |
|---|---|
| 백준 20176 Needle (3) | 2021.06.23 |
| 백준 1014번 컨닝 (0) | 2021.05.17 |
| 백준 1086 박성원 (0) | 2021.05.16 |
| 백준 1946번 신입사원 (0) | 2020.08.05 |
문제
S는 다음과 같이 정의된다.
- S(0, n) = n (모든 양의 정수 n)
- S(k, n) = S(k-1, 1) + S(k-1, 2) + ... + S(k-1, n) (모든 양의 정수 k, n)
k와 n이 주어졌을 때, S(k, n)을 1,000,000,007로 나눈 나머지를 구하는 프로그램을 작성하시오.
풀이
이 문제같은 경우 어떤 성질을 이용해 점화식을 도출하고 ... 라는 일련의 과정보단, 직접 써보는 것이 이해가 빠를 것이다.

직접 써보니 이런 식의 표가 나왔다.
실제로 문제의 수식대로 저기까지만 계산해도 상당히 머리아픈데, 사람은 귀찮은걸 싫어하다보니.. 저거 쓰는 과정에서도 수를 빨리 도출해내는 법을 찾게 된다. 쓰다 보면 금방 찾는 규칙인데, 규칙은 다음과 같다.

파란색 원 안의 수는 그 수 기준 왼쪽과 위쪽 빨간색 수의 합으로 나타낼 수 있다는 점이다.
이 부분은 생각해보면 간단한데, A[n][k] = A[n][k-1] + A[n-1][k-1] + ... + A[1][k-1] 이라는 속성을 표에 표시해보면

이런 식으로 나타낼 수 있고, 마지막 1은 n이 1일 때 모두 동일하므로 바꿔줄 수 있다.
즉, A[n][k] = A[n][k-1] + A[n-1][k]
그런데 이와 같은 경우, 문제에서 나오는 n이 최대 10억이므로 도저히 계산할 수 없는 지경에 이를 수 있다.
하지만 우리는 위에서 해당 유형을 몇 가지 풀어봤고, 문제 조건에서 주어지는 어떤 수의 제한이 50이라면?
좀 느낌이 다르게 느껴진다. 50 x 50 행렬은 충분히 이 유형에 쓰일 수 있기 때문이다.
따라서 저 공식을 k에 맞춰 다시 고쳐볼 수 있다. (불편하면 자세를 고쳐 앉으세요..!)

이렇게 가로로 눕혀놓는다면, n이 아무리 크더라도, k제한은 50이기 때문에 식이 확 줄어들게 된다.
이제 행렬로 표현해볼 건데, 이해를 돕기 위해 몇 가지 식만 적어본다.
- (3, 0) = (2, 0) + 1
- (3, 1) = (2, 1) + (2, 0) + 1
- (3, 2) = (2, 2) + (2, 1) + (2, 0) + 1
- (4, 2) = (3, 2) + (3, 1) + (3, 0) + 1
- (n, k) = (n-1, k) + ... + (n-1, 0) + 1
행렬로 나타내면 다음과 같다.

마지막으로 우리가 아는 행렬 거듭제곱으로 시각화한다면 다음과 같다.

소스 코드(.cpp)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll ans[55][55];
ll arr[55][55];
int k, n;
const int MOD = 1000000007;
void mul(ll A[55][55], ll B[55][55]) {
ll ret[55][55] = { 0, };
for (int i = 0; i < k+2; i++) {
for (int j = 0; j < k+2; j++) {
for (int a = 0; a < k+2; a++) {
ret[i][j] = (ret[i][j] + (A[i][a] * B[a][j])) % MOD;
}
}
}
for (int i = 0; i < 55; i++) {
for (int j = 0; j < 55; j++) {
A[i][j] = ret[i][j];
}
}
}
int main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> k >> n;
for (int i = 0; i < k + 2; i++) ans[i][i] = 1;
for (int i = 0; i < k + 2; i++) {
for (int j = 0; j <= i; j++) {
arr[i][j] = 1;
}
}
n--;
while (n > 0) {
if (n % 2 == 1) mul(ans, arr);
mul(arr, arr);
n /= 2;
}
ll sum = 0;
for (int i = 0; i < k + 2; i++) {
sum = (sum + ans[k + 1][i]) % MOD;
}
cout << sum << "\n";
return 0;
}'백준 문제풀이' 카테고리의 다른 글
| 백준 20173번 Imprecise Computer (1) | 2021.07.08 |
|---|---|
| 백준 20176 Needle (3) | 2021.06.23 |
| 백준 1014번 컨닝 (0) | 2021.05.17 |
| 백준 1086 박성원 (0) | 2021.05.16 |
| 백준 1946번 신입사원 (0) | 2020.08.05 |
