제목을 잘못 적은 게 아니라, 문제 이름이 박성원이다.. 심지어 solved ac 공식 standard 문제!
풀이
이 문제는 3가지 부분 문제가 포함되어 있다고 볼 수 있다.
- 무려 길이가 최대 50인 자연수에 K로 나눈 나머지를 어떻게 구할 것인가
- 기약 분수 형태 출력은 어떻게 하는 게 빠를까?
- 위에 두 개 알았는데.. 그래서 어떻게 푸는데..?
우선 하나씩 해결해보자.
1. 큰 수(BigInteger) 나누기
우린 초등학교 3학년 때 구구단을 외우고, 4학년 때 나누는 방법을 배운다.
초4 수환이 큰 수 111111을 3으로 나누면 이런 방식으로 나눌 것이다.
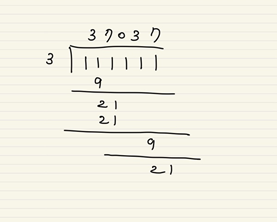
이 과정을 살짝 프로그래밍적으로 분석하면 과정은 이러하다.
- 가장 앞자리 (자릿수가 가장 큰)부터 시작한다.
- 갖고 있는 수에 10을 곱한 후, 현재 자리에 있는 수를 더한다.
- 만약 현재 제수(divisor) 보다 갖고 있는 수가 크다면, 갖고 있는 수를 제수로 나눈 몫이 위로 올라가고, 나머지는 갖고 있는 수가 된다.
- 3번을 거쳤거나, 작다면 다시 2번으로 되돌아간다.
- 이 과정을 가장 마지막 자릿수까지 반복한다.
일반적으로 우리가 "/" 기호를 사용하면 이 과정이 자동으로 O(1) 시간에 해결되지만, 만약 수가 10^50이라면 우리는 이 수를 문자열로 받고, 위 과정을 수작업으로 해줘야 한다.
그렇지만 생각보다 어렵지 않고 시간 복잡도는 O(|S|) (|S| : 문자열 길이)가 된다.
예시 코드
//x를 k로 나눈 나머지 반환
int rem(string x) {
int tmp = 0;
for (int i = 0; i < x.size(); i++) {
tmp *= 10;
tmp += x[i] - '0';
tmp %= k;
}
return tmp;
}
2. 기약 분수 출력
나름 웰노운하지만, 이 글을 보시는 분들은 아주 다양하니 스킵하지 않고 설명을 적도록 하겠다.
만약 기약 분수가 아닌 분수 P/Q 가 있을 때, 기약 분수로 만드는 방법은 간단하다.
P, Q의 최대 공약수를 구한 후, P, Q 각각을 최대 공약수로 나누어주면 된다.
최대 공약수는 유클리드 호제법에 의해서 log(P + Q) 이므로 이 부분은 어떤 수가 나와도 대부분 가능하다.
* 참고) 유클리드 호제법 최대 공약수 구하는 코드
소스 코드(.cpp)
int gcd(int a, int b) {
if (b == 0) return a;
else return gcd(b, a % b);
}
3. 이제 어떡하지..
문제에서 주어지는 집합의 수의 개수 N은 최대 15라서 모든 순열을 구하면 15! 가짓수가 된다.
참고로 보통 우리가 팩토리얼 시간 복잡도를 계산할 때 12! 부터는 1억이 가볍게 넘어가므로 안된다고 생각하는 게 좋다.
그럼 모든 가짓수를 일일이 계산하지 않고도 구할 수 있는 방법을 생각해봐야 한다.
내가 생각하던 중 떠오른 아이디어는 이렇다.
- (k로 나누어 떨어지는 수)를 여러 개 막 붙여도 k로 나누어 떨어지는구나!
- k가 3이고, 어떤 수 A라 할 때 3으로 나눈 나머지가 1인 수 (1, 4, 7, 10,...)를 A 뒤에 붙여도 k로 나눈 나머지는 똑같구나!
나는 첫 번째 아이디어에서 시작해 두 번째 아이디어로 왔었다.
그렇다면 이 아이디어에서 우리는 시간을 줄일 수 있는 방법을 생각해볼 수 있는데
방법은 이렇다.
굳이 모든 순열을 구해줄 필요 없이, 순서를 기록할 필요 없이 현재까지 어떤 수들을 골라 붙여놨고, 그 수들의 조합이 형성한 나머지의 개수를 알면 다음 수를 붙일 때 (나머지 + 다음수) 끼리 붙으니 나머지들을 고려해서 바로바로 구해줄 수 있다는 것이다.
말이 어려울 수 있는데.. dp table을 만들어보면 이런 식이다.
- dp[i][j] : 현재 상태(i)에서 k로 나눈 나머지가 j인 순열의 가짓수
이때, 현재 상태 i는 N이 최대 15이므로 비트로 표현할 수 있는데
만약 N이 3이고 첫 번째 수만 골랐다면 100
모든 수를 골랐다면 111
두 번째 수만 골랐다면 010
... 이런 식으로 표현하는 방법이다. 총 2^15(약 3만) 가지로, 생각보다 큰 수는 아니다.
그렇다면 문제에서 예제 케이스 집합 {3, 2, 1} 이 주어졌을 때 모든 수를 고른 dp table의 상태는 이렇다.
dp[7][0] = 2 ({1,3,2}, {3,1,2}) (비트 "111" = 7)
dp[7][1] = 4 (이외 나머지)
만약 이 상태에서 집합의 맨 앞에 "4"라는 수가 추가될 때 ({4, 3, 2, 1}) dp table의 변화는 이렇다.
dp[7][0] -> 0에 4를 추가하면 나누어 떨어짐, dp[5 + (1<<4)][0] += dp[5][0]
dp[7][1] -> 1에 4를 붙여도 여전히 나머지 1, dp[5 + (1<<4)][1] += dp[5][1]
만약 "3"이라는 수를 추가하면 반대로 dp[i+1][0] 에 dp[i][1] 이 추가될 것이다.
이런 식으로 그 전 상태의 나머지와 현재의 수를 붙여서 현재 상태 dp table을 완성시켜주면 된다.
시간 복잡도는 우선 dp table 만큼 O(2^N x K)에 각 상태마다 다음 상태를 선정 (다음 수를 고르기) 하는 데 N번 반복되므로 총 O(2^N x N x K) 이 되겠다.
소스 코드(.cpp)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n, k;
vector<string>a;
//dp[i][j] : 특정 비트로 구성된 수들 중 k로 나눈 나머지가 j인 경우의 수
ll dp[1<<15][101];
// 각 수(1개)를 k로 나눈 나머지
ll remd[20];
// 비트로 구성된 수들을 k로 나눈 나머지
ll lenRem[51];
//x를 k로 나눈 나머지 반환
int rem(string x) {
int tmp = 0;
for (int i = 0; i < x.size(); i++) {
tmp *= 10;
tmp += x[i] - '0';
tmp %= k;
}
return tmp;
}
ll gcd(ll a, ll b) {
if (b == 0) return a;
else return gcd(b, a % b);
}
int main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> n;
for (int i = 0; i < n; i++) {
string x; cin >> x;
a.push_back(x);
}
cin >> k;
//나머지 전처리
for (int i = 0; i < n; i++) {
remd[i] = rem(a[i]);
}
lenRem[0] = 1 % k;
for (int i = 1; i <= 50; i++) {
lenRem[i] = (lenRem[i - 1] * 10) % k;
}
dp[0][0] = 1;
//비트 순회
for (int num = 0; num < (1 << n); num++) {
//하나씩 수를 고른다
for (int i = 0; i < n; i++) {
//현재 비트에 갖고 있지 않은 수이면
if ((num & (1 << i)) == 0) {
int next = (num | (1 << i));
//해당 비트 나머지 검사
for (int j = 0; j < k; j++) {
int nextRem = ((j * lenRem[a[i].size()]) % k + remd[i]) % k;
dp[next][nextRem] += dp[num][j];
}
}
}
}
ll bunza = 1, bunmo = 1;
for (int i = 1; i <= n; i++) bunmo *= i;
bunza = dp[(1 << n) - 1][0];
ll gcdNum = gcd(bunza, bunmo);
cout << bunza / gcdNum << "/" << bunmo / gcdNum << "\n";
return 0;
}
'백준 문제풀이' 카테고리의 다른 글
| 백준 13430번 합 구하기 (0) | 2021.05.24 |
|---|---|
| 백준 1014번 컨닝 (0) | 2021.05.17 |
| 백준 1946번 신입사원 (0) | 2020.08.05 |
| 백준 5052번 전화번호 목록 (0) | 2020.05.06 |
| 백준 9252번 LCS 2 (0) | 2020.02.12 |
제목을 잘못 적은 게 아니라, 문제 이름이 박성원이다.. 심지어 solved ac 공식 standard 문제!
풀이
이 문제는 3가지 부분 문제가 포함되어 있다고 볼 수 있다.
- 무려 길이가 최대 50인 자연수에 K로 나눈 나머지를 어떻게 구할 것인가
- 기약 분수 형태 출력은 어떻게 하는 게 빠를까?
- 위에 두 개 알았는데.. 그래서 어떻게 푸는데..?
우선 하나씩 해결해보자.
1. 큰 수(BigInteger) 나누기
우린 초등학교 3학년 때 구구단을 외우고, 4학년 때 나누는 방법을 배운다.
초4 수환이 큰 수 111111을 3으로 나누면 이런 방식으로 나눌 것이다.
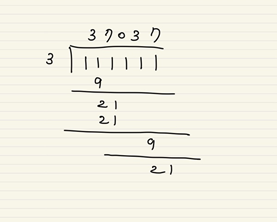
이 과정을 살짝 프로그래밍적으로 분석하면 과정은 이러하다.
- 가장 앞자리 (자릿수가 가장 큰)부터 시작한다.
- 갖고 있는 수에 10을 곱한 후, 현재 자리에 있는 수를 더한다.
- 만약 현재 제수(divisor) 보다 갖고 있는 수가 크다면, 갖고 있는 수를 제수로 나눈 몫이 위로 올라가고, 나머지는 갖고 있는 수가 된다.
- 3번을 거쳤거나, 작다면 다시 2번으로 되돌아간다.
- 이 과정을 가장 마지막 자릿수까지 반복한다.
일반적으로 우리가 "/" 기호를 사용하면 이 과정이 자동으로 O(1) 시간에 해결되지만, 만약 수가 10^50이라면 우리는 이 수를 문자열로 받고, 위 과정을 수작업으로 해줘야 한다.
그렇지만 생각보다 어렵지 않고 시간 복잡도는 O(|S|) (|S| : 문자열 길이)가 된다.
예시 코드
//x를 k로 나눈 나머지 반환
int rem(string x) {
int tmp = 0;
for (int i = 0; i < x.size(); i++) {
tmp *= 10;
tmp += x[i] - '0';
tmp %= k;
}
return tmp;
}
2. 기약 분수 출력
나름 웰노운하지만, 이 글을 보시는 분들은 아주 다양하니 스킵하지 않고 설명을 적도록 하겠다.
만약 기약 분수가 아닌 분수 P/Q 가 있을 때, 기약 분수로 만드는 방법은 간단하다.
P, Q의 최대 공약수를 구한 후, P, Q 각각을 최대 공약수로 나누어주면 된다.
최대 공약수는 유클리드 호제법에 의해서 log(P + Q) 이므로 이 부분은 어떤 수가 나와도 대부분 가능하다.
* 참고) 유클리드 호제법 최대 공약수 구하는 코드
소스 코드(.cpp)
int gcd(int a, int b) {
if (b == 0) return a;
else return gcd(b, a % b);
}
3. 이제 어떡하지..
문제에서 주어지는 집합의 수의 개수 N은 최대 15라서 모든 순열을 구하면 15! 가짓수가 된다.
참고로 보통 우리가 팩토리얼 시간 복잡도를 계산할 때 12! 부터는 1억이 가볍게 넘어가므로 안된다고 생각하는 게 좋다.
그럼 모든 가짓수를 일일이 계산하지 않고도 구할 수 있는 방법을 생각해봐야 한다.
내가 생각하던 중 떠오른 아이디어는 이렇다.
- (k로 나누어 떨어지는 수)를 여러 개 막 붙여도 k로 나누어 떨어지는구나!
- k가 3이고, 어떤 수 A라 할 때 3으로 나눈 나머지가 1인 수 (1, 4, 7, 10,...)를 A 뒤에 붙여도 k로 나눈 나머지는 똑같구나!
나는 첫 번째 아이디어에서 시작해 두 번째 아이디어로 왔었다.
그렇다면 이 아이디어에서 우리는 시간을 줄일 수 있는 방법을 생각해볼 수 있는데
방법은 이렇다.
굳이 모든 순열을 구해줄 필요 없이, 순서를 기록할 필요 없이 현재까지 어떤 수들을 골라 붙여놨고, 그 수들의 조합이 형성한 나머지의 개수를 알면 다음 수를 붙일 때 (나머지 + 다음수) 끼리 붙으니 나머지들을 고려해서 바로바로 구해줄 수 있다는 것이다.
말이 어려울 수 있는데.. dp table을 만들어보면 이런 식이다.
- dp[i][j] : 현재 상태(i)에서 k로 나눈 나머지가 j인 순열의 가짓수
이때, 현재 상태 i는 N이 최대 15이므로 비트로 표현할 수 있는데
만약 N이 3이고 첫 번째 수만 골랐다면 100
모든 수를 골랐다면 111
두 번째 수만 골랐다면 010
... 이런 식으로 표현하는 방법이다. 총 2^15(약 3만) 가지로, 생각보다 큰 수는 아니다.
그렇다면 문제에서 예제 케이스 집합 {3, 2, 1} 이 주어졌을 때 모든 수를 고른 dp table의 상태는 이렇다.
dp[7][0] = 2 ({1,3,2}, {3,1,2}) (비트 "111" = 7)
dp[7][1] = 4 (이외 나머지)
만약 이 상태에서 집합의 맨 앞에 "4"라는 수가 추가될 때 ({4, 3, 2, 1}) dp table의 변화는 이렇다.
dp[7][0] -> 0에 4를 추가하면 나누어 떨어짐, dp[5 + (1<<4)][0] += dp[5][0]
dp[7][1] -> 1에 4를 붙여도 여전히 나머지 1, dp[5 + (1<<4)][1] += dp[5][1]
만약 "3"이라는 수를 추가하면 반대로 dp[i+1][0] 에 dp[i][1] 이 추가될 것이다.
이런 식으로 그 전 상태의 나머지와 현재의 수를 붙여서 현재 상태 dp table을 완성시켜주면 된다.
시간 복잡도는 우선 dp table 만큼 O(2^N x K)에 각 상태마다 다음 상태를 선정 (다음 수를 고르기) 하는 데 N번 반복되므로 총 O(2^N x N x K) 이 되겠다.
소스 코드(.cpp)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n, k;
vector<string>a;
//dp[i][j] : 특정 비트로 구성된 수들 중 k로 나눈 나머지가 j인 경우의 수
ll dp[1<<15][101];
// 각 수(1개)를 k로 나눈 나머지
ll remd[20];
// 비트로 구성된 수들을 k로 나눈 나머지
ll lenRem[51];
//x를 k로 나눈 나머지 반환
int rem(string x) {
int tmp = 0;
for (int i = 0; i < x.size(); i++) {
tmp *= 10;
tmp += x[i] - '0';
tmp %= k;
}
return tmp;
}
ll gcd(ll a, ll b) {
if (b == 0) return a;
else return gcd(b, a % b);
}
int main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> n;
for (int i = 0; i < n; i++) {
string x; cin >> x;
a.push_back(x);
}
cin >> k;
//나머지 전처리
for (int i = 0; i < n; i++) {
remd[i] = rem(a[i]);
}
lenRem[0] = 1 % k;
for (int i = 1; i <= 50; i++) {
lenRem[i] = (lenRem[i - 1] * 10) % k;
}
dp[0][0] = 1;
//비트 순회
for (int num = 0; num < (1 << n); num++) {
//하나씩 수를 고른다
for (int i = 0; i < n; i++) {
//현재 비트에 갖고 있지 않은 수이면
if ((num & (1 << i)) == 0) {
int next = (num | (1 << i));
//해당 비트 나머지 검사
for (int j = 0; j < k; j++) {
int nextRem = ((j * lenRem[a[i].size()]) % k + remd[i]) % k;
dp[next][nextRem] += dp[num][j];
}
}
}
}
ll bunza = 1, bunmo = 1;
for (int i = 1; i <= n; i++) bunmo *= i;
bunza = dp[(1 << n) - 1][0];
ll gcdNum = gcd(bunza, bunmo);
cout << bunza / gcdNum << "/" << bunmo / gcdNum << "\n";
return 0;
}
'백준 문제풀이' 카테고리의 다른 글
| 백준 13430번 합 구하기 (0) | 2021.05.24 |
|---|---|
| 백준 1014번 컨닝 (0) | 2021.05.17 |
| 백준 1946번 신입사원 (0) | 2020.08.05 |
| 백준 5052번 전화번호 목록 (0) | 2020.05.06 |
| 백준 9252번 LCS 2 (0) | 2020.02.12 |
