프로그래밍 입문 수업 - 소수 판별법

기업 코딩 테스트 2~3번 단골 문제 중 하나인
N 이하의 소수(prime number)를 모두 찾아내는 방법에 대해 알아봅시다!

이 문제 유형은 대체로 백준 실버 1~2에 포진되어 있고 "문제는 어려우나, 이론은 간단한" 유형에 속합니다.
(백준 1929 소수 구하기 : https://www.acmicpc.net/problem/1929)

이 유형은 "에라토스테네스의 체" 알고리즘을 알면 풀 수 있고, 모르면 못 푸는 문제인데요
에라토스테네스의 체란 고운 가루는 체에 걸러 통과시킨다는 뜻을 가지고 있는데, 여기서 고운 가루는 소수를 의미하게 됩니다.
(이때 소수란 1과 자기 자신만 약수로 가지는 수를 의미합니다!)

에라토스테네스의 체에 대해서는 천천히 알아보고, 우선 일반적인 방법부터 살펴볼게요.

1) 일반적인 방법

일반적인 소수 판별법은 시간 복잡도 O(N^2) 이 걸리는, 1 ~ N의 모든 수에 대해서, 어떤 X가 2~X-1에서 자신과 나누어 떨어지지는 수가 하나도 존재하지 않으면 X는 소수라고 판별할 수 있는 방법입니다.
예를 들어 소수 7은 2~6까지 어떤 수도 7과 나누어 떨어지지 않지만, 6은 2, 3이 6의 약수이기 때문에 나누어 떨어집니다.
이 방법은 가장 쉽게 떠올릴 수 있는 방법으로, 구간을 구하려면 N이 10,000 이하여야 시간제한 1초의 문제를 통과할 수 있습니다.

예시 코드

#include <stdio.h>
#include <math.h> 
#include <stdbool.h>
int main(void) { 
	int N; 
    scanf("%d", &N);
    for(int i=2; i<=N; i++){ 
    	//i가 소수인지 확인하는 과정 
        bool Isprime = true;
        for(int j=2; j<=N; j++){ 
        	//만약 i를 j로 나눈 나머지가 0이면, i는 소수가 될 수 없다. 
            Isprime = false;
        }
        
        if(Isprime) printf("%d ", i);
    } 
    return 0;
}

2) 개선된 방법

X가 소수인지 아닌지를 판별하기 위해선 굳이 X-1까지 약수를 검증할 필요가 없습니다.
12라는 합성수(소수가 아닌 수)를 판별할 때 2, 3, 4, 6 은 모두 위의 방법에서 걸러지게 됩니다. (12로 나누어 떨어지므로)
하지만 2는 12가 되기 위해선, 6과 합성(곱하기)되어야 하기 때문에 굳이 6을 볼 필요가 없게 됩니다.

예를 들어 소수 11을 확인할 때, 굳이 4이상은 볼 필요가 없다는 것이죠.
(2,3은 이미 약수가 아닌 상태에다가, 4가 합성수이려면 4 이상의 다른 수와 곱해 11이 나와야 하는데, 그 수는 최소 16이 될 것이기 때문입니다.)

따라서 교수님 문제 방식대로, 양의 정수 N의 양의 제곱근 이하의 수들로 N을 나누어 한 번이라도 나누어 떨어지면 합성수, 아니면 소수라고 판정하는 방법이 단일 X가 소수인지 아닌지를 판별할 때 가장 좋은 방법입니다. 시간 복잡도 : O(N * sqrt(N))
(이 방법은 당장 올해 9월에 실시된 카카오 1차 코딩테스트 2번 문제에 그대로 등장했습니다!)

하지만 여러 구간의 수가 소수인지 아닌지를 판별하기 위해서는 또 다른 방법을 사용해야 합니다.
위 시간 복잡도 상으로 시간제한 1초만에 구할 수 있는 수는 많아야 5만? 정도일 텐데, 문제는 100만 정도 구간을 잡고 나옵니다.

예시 코드

#include <stdio.h>
#include <math.h> 
#include <stdbool.h>
int main(void) { 
	int N; 
    scanf("%d", &N);
    for(int i=2; i<=N; i++){ 
    	//i가 소수인지 확인하는 과정 
        bool Isprime = true;
        for(int j=2; j<=sqrt(N); j++){ 
        	//만약 i를 j로 나눈 나머지가 0이면, i는 소수가 될 수 없다. 
            Isprime = false;
        }
        
        if(Isprime) printf("%d ", i);
    } 
    return 0;
}

3) 에라토스테네스의 체 방법

앞에서 설명드렸듯, 에라토스테네스의 체는 수를 걸러내는 역할을 하는데 우선 1은 제외하고 합성수들을 걸러내 줍시다.
이때 편의상 전체 수 N은 50으로 하겠습니다.

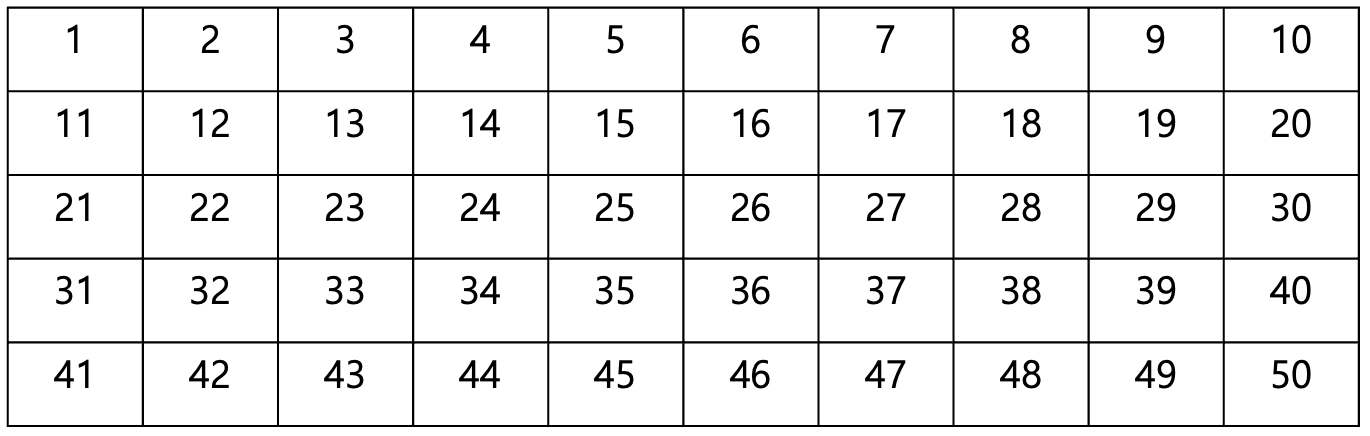
우선 1을 제외해줍시다.

이제부터 순서대로 빨간색이 되지 않은 수를 만나면 해당 수를 제외한 배수들을 모두 빨간색으로 칠해주는 과정을 반복합니다.
2는 색칠이 되지 않았기 때문에 2를 제외한 2의 배수들을 모두 칠해줍니다.

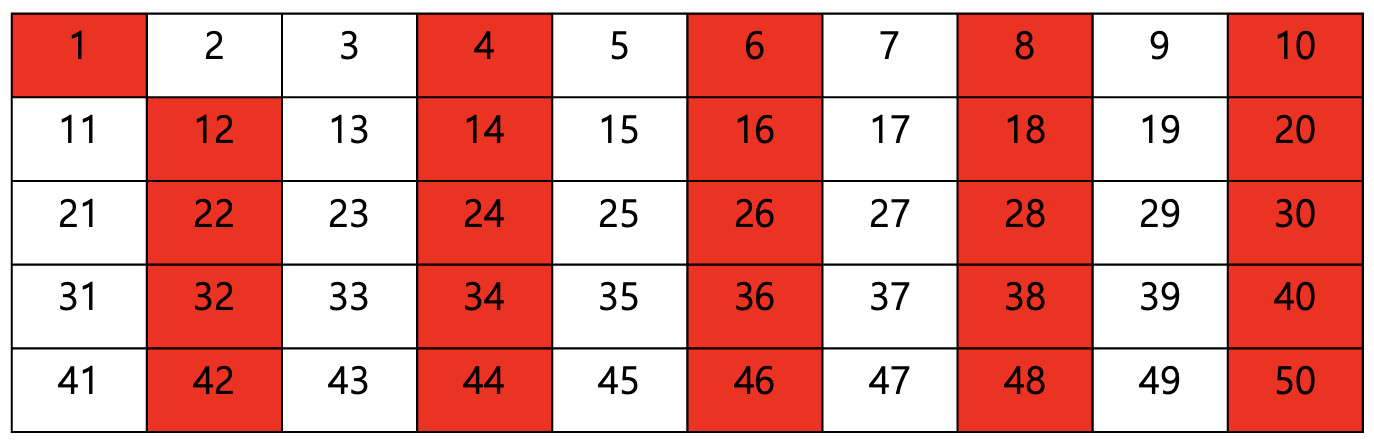
다음은 3을 제외한 3의 배수들을 모두 칠해줍니다.

다음 수 4는 이미 색칠되어있기 때문에 건너뛰고, 5를 제외한 5의 배수들을 모두 칠해줍니다.

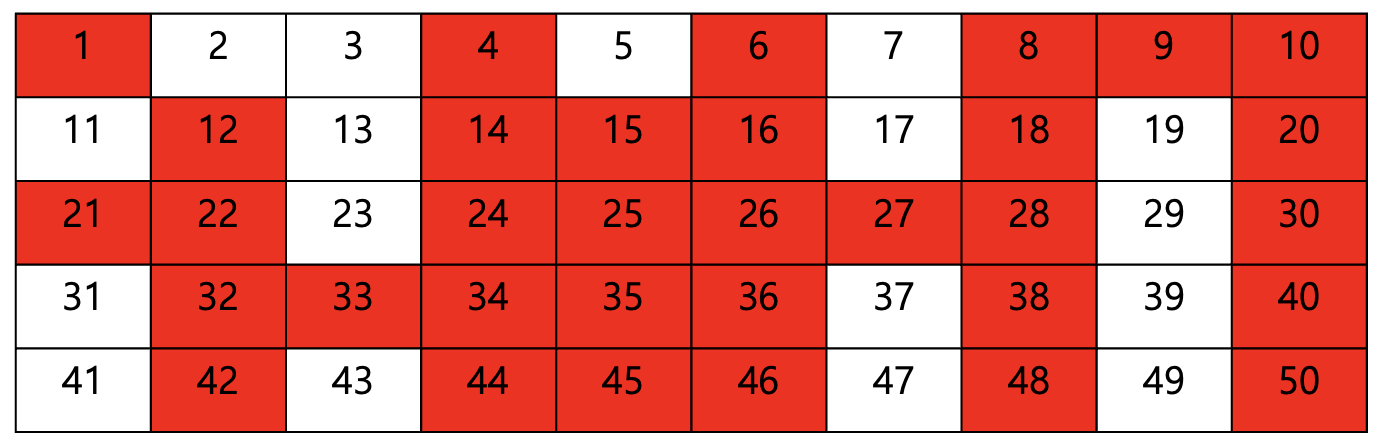
마지막으로 7을 제외한 7의 배수들을 모두 칠해줍니다.

50의 루트 값은 7.xxx 이므로 7의 배수들까지만 확인을 했다면 위에서 설명한 2번 "개선된 방법"과 같은 이유로 다음 배수들은 볼 필요가 없습니다. 따라서 위에서 색칠되지 않은 수들은 50 이하의 모든 소수들을 의미하게 됩니다.

이 알고리즘의 시간 복잡도는 상당히 어려운 수학적 지식을 요구하기 때문에 이해하기 힘들고, 소수를 구하는 문제에서 이보다 좋은 방법은 일반적인 문제에서 요구하지 않기 때문에 이 정도만 알아두셔도 충분합니다. 따라서 시간복잡도는 O(NloglogN)입니다.


예시 코드

#include <stdio.h>
#include <math.h>
#include <stdbool.h>
int main(void) { 
	int N;
    scanf("%d", &N);
    //소수이면 true, 소수가 아니면 false 
    bool IsPrime[1000001];
    
    //미리 모두 true로 바꾸어줍니다.
    for(int i=2; i<=1000000; i++) IsPrime[i] = true; 
    
    for(int i=2; i<=sqrt(N); i++){ 
    	//i가 소수인지 확인하는 과정 
        if(IsPrime[i] == true){ 
        	//i의 배수를 찾기위해, i부터 시작하여 i를 계속 더해줍니다. 
            for(int j=i + i; j<=N; j+=i){ 
            	// 이때 나오는 j는 전부 i를 포함한 합성수입니다. 
                IsPrime[j] = false; 
            }
        } 
    }
    
    for(int i=2; i<=1000000; i++){
    	if(Isprime[i]) printf("%d ", i);
    }
    return 0;
}

 

 

관련 문제

• 백준 1929번 소수 구하기 - https://www.acmicpc.net/problem/1929
• 백준 4948번 베르트랑 공준 - https://www.acmicpc.net/problem/4948
• 백준 6588번 골드바흐의 추측 - https://www.acmicpc.net/problem/6588