그리디 알고리즘(Greedy Algorithm)은 "탐욕적인"이라는 뜻의 greedy에서 유래된 알고리즘이다.
다른 말로 "욕심쟁이 기법" 이라고도 부르는데
만약 여러 노드를 갖는 그래프에서 A노드 -> B노드까지의 경로를 탐색하려 할 때 모든 경로를 고려하지 않고
단지, 현재의 위치(노드)에서 가장 최적의 경로(예를 들면 에지의 가중치가 작은) 를 도착지까지 매 순간마다 가장 좋은 방법만을 선택하는 방법이다.
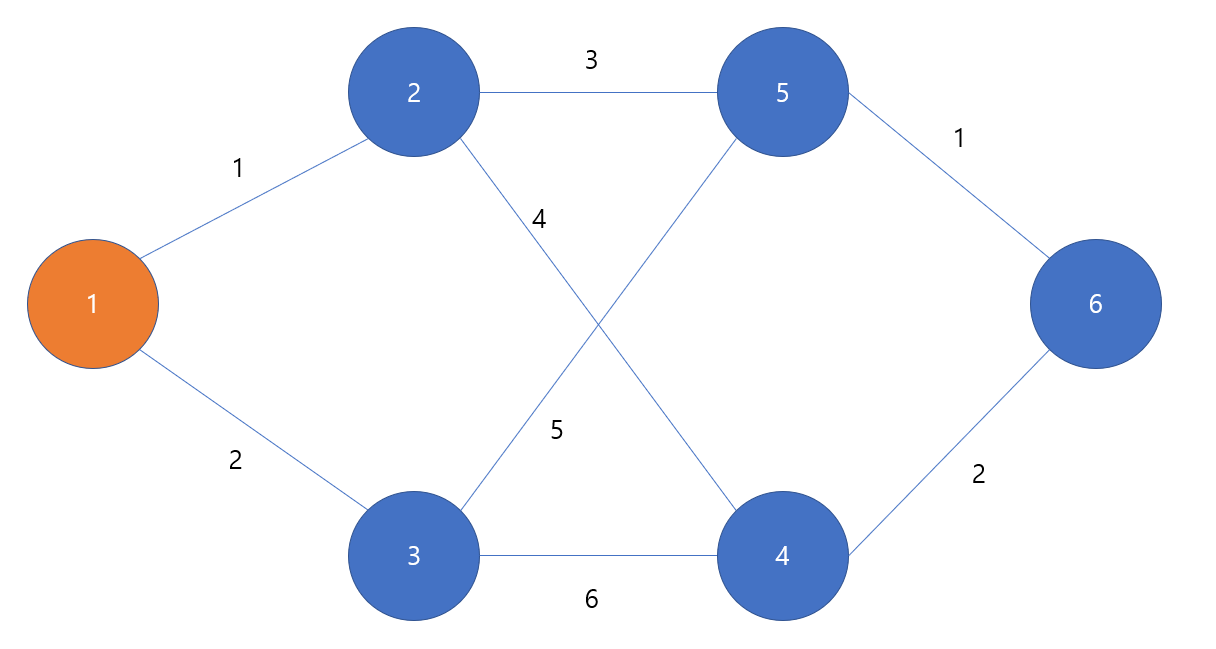
다익스트라 알고리즘도 그리디 알고리즘의 한 예시인데
간단히 설명하자면, 한 노드를 시작점으로 출발해 목적지에 연결될 때 까지 현재 연결된 노드로부터
연결된 에지들의 가중치 중 최소만을 선택하는 방법을 말한다. (사이클이 생기지 않는 선에서)
만약 위 그림에서 노드 1->6 까지의 최단 거리를 구하는 문제를 다익스트라 알고리즘을 통해 풀어보자면,
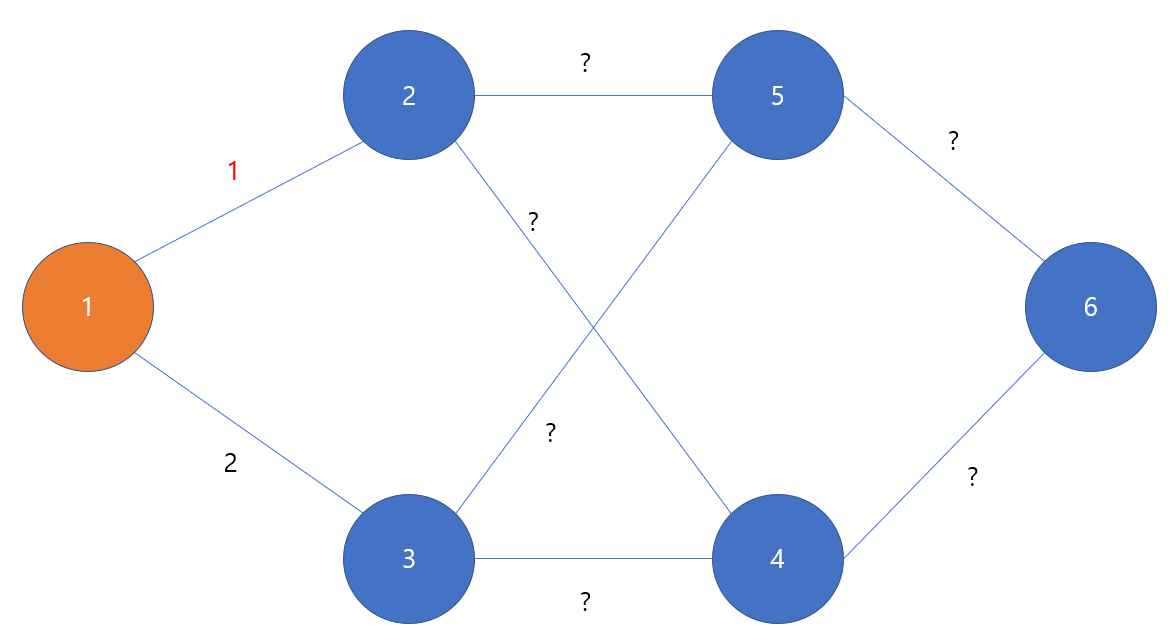
맨 처음 우리가 선택할 수 있는 경로는 1->2, 1->3 둘 뿐이다.
우린 "탐욕적인" 방법을 선택하였기 때문에 둘 중 가중치가 더 적은 1->2 에지를 선택하게 된다.

2번 노드에 도착했기 때문에 이제 2번 노드와 연결된 에지들도 고려해야 한다.
이제 1->3, 2->5, 2->4 총 3가지의 에지들이 있는데, 이 중 가장 최단인 1->3 에지를 선택하게 된다.
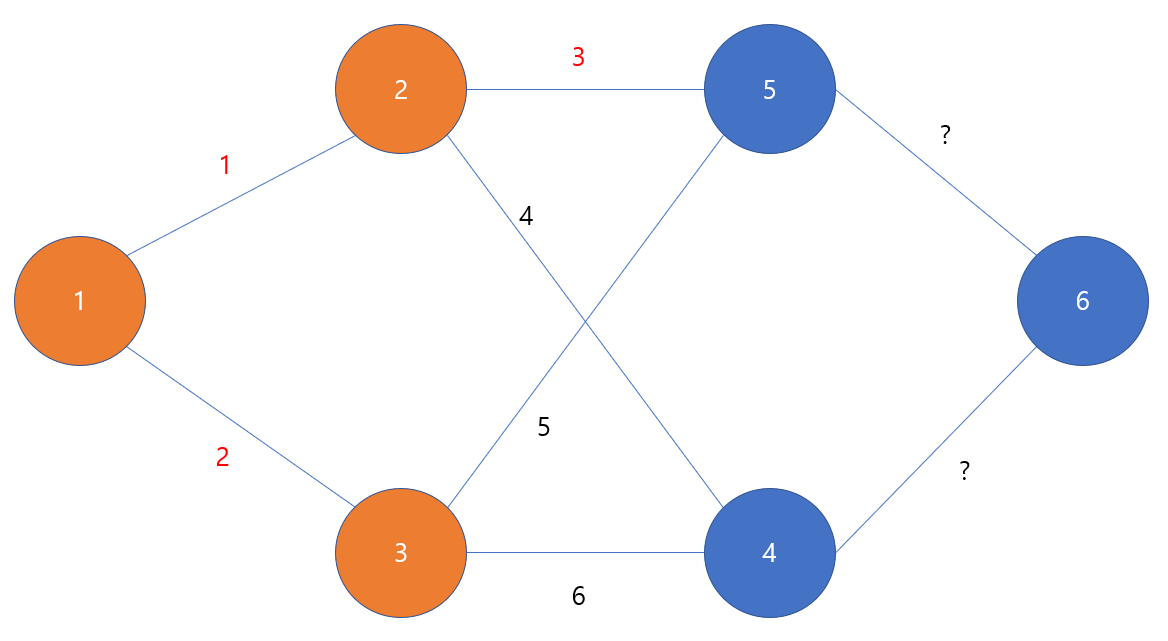
이제 3번 노드를 획득했고,
우리가 알고 있는 에지들은 2->5, 2->4, 3->5, 3->4 가 있어서 가장 최단인 2->5 에지를 선택한다.
이런 방법을 통해 최단 경로를 구하게 되면
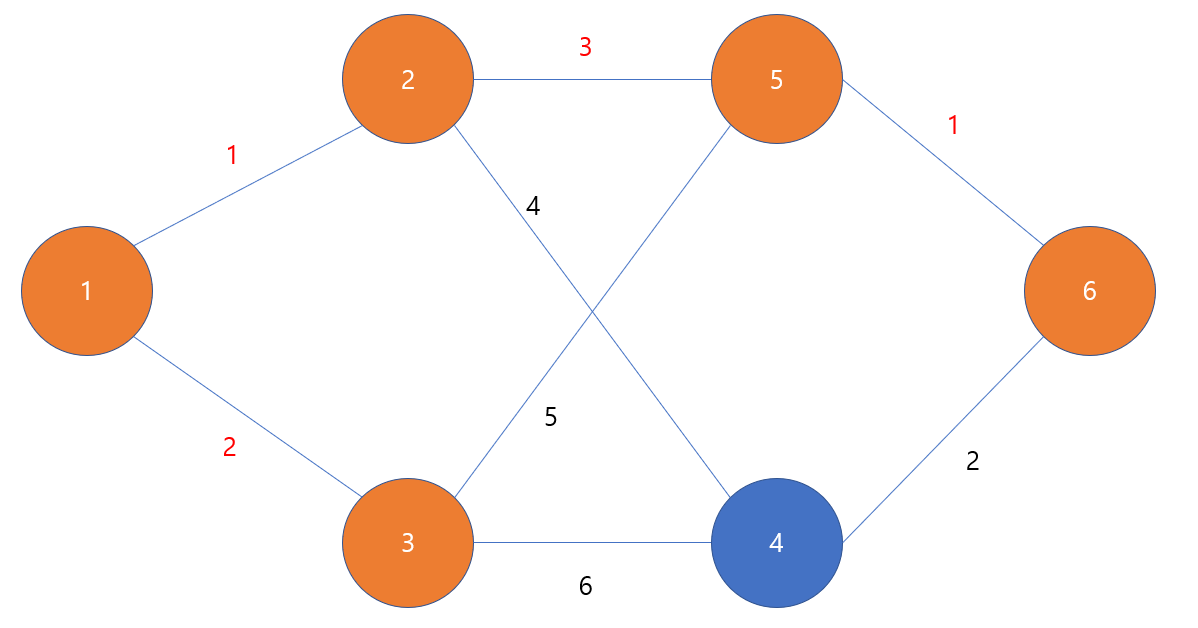
1->2->5->6으로 이어지는 거리 5의 최단거리를 구할 수 있게 된다.
하지만 이는 잘 알려진 다익스트라 알고리즘 안의 그리디 알고리즘이고
실제로 우리가 문제를 풀 때에는 그리디를 생각해내기 쉽지 않고, 많은 경우 그리디로 풀면 되겠다! 싶은데
실제로 풀면 최적해를 찾지 못하여 틀리는 경우도 있고, 풀었으나 왜 이게 최적인지 확실하게 증명하지 못하는 경우가 많다.
따라서 적용하기 전 그리디 알고리즘의 정당성을 검증해 봐야 한다.
그리디 알고리즘의 두 가지 증명
1. 탐욕적 선택 속성(greedy choice property)
2. 최적 부분 구조(optimal substructure)
1. 탐욕적 선택 속성(greedy choice property) 은 동적 계획법처럼 답의 모든 부분을 고려하지 않고 탐욕적으로만
선택하더라도 최적해를 구할 수 있다는 것을 의미한다.
즉, 앞에서 탐욕적인 선택을 해서 "손해"를 볼 일이 없어야 한다.
2. 최적 부분 구조(optimal substructure)는 탐욕적으로 선택한 매 순간의 결과가 전체 문제의 최적이어야 한다.
만약 눈앞에 보이는 빠른 길만을 이용해 도착점에 도달했는데, 시작점에서 도착점으로 바로 가는 지름길이 더 빠른경우 탐욕적으로 선택하면 안된다는 것이다.
그리디 알고리즘의 어려움
많은 고수분들은 그리디 알고리즘을 어렵다고 한다.
실제로 대회에서도 그리디 알고리즘으로 생각되는 문제를 가장 나중에 푼다고도 한다.
그리디 알고리즘은 개념은 간단하지만, 그리디 문제를 막상 마주쳤을 때 문제에 여러 조건이 있기 때문에
바로 "이 부분을 최적화하면 해결할 수 있어!"라고 바로 떠오르지 않고, 심지어 풀이는 직관적이나,
문제에 대한 접근이 직관적이지 않기 때문에 함정에 빠지기 십상이다.
따라서 그리디 알고리즘을 연습할 때는 알고리즘의 정당성을 증명하는 과정을 항상 연습하는 것이 필요하다.
그리디 알고리즘과 동적 계획법
입력 조건이 까다롭지 않은 경우 그리디 알고리즘으로 풀 수 있는 문제는 동적 계획법으로 해결 가능하다.
당연하게도 동적 계획법은 모든 경우를 다 고려하기 때문에 메모리나 시간이 초과되지 않는 선에서는 동적 계획법이 더 많이 생각날 것이다.
하지만 역으로 생각해보면 입력 조건이 상당히 까다로운 경우 그리디 알고리즘을 사용하라는 출제자의 힌트가 될 수도 있으니 관련 문제를 많이 풀어봐야 할 것이다.
그리디 알고리즘 풀이 순서
이 풀이 순서는 종만북에 쓰여있는 "탐욕적 알고리즘 레시피" 를 인용하였습니다.
- 문제의 답을 만드는 과정을 여러 조각으로 나눈다.
- 각 조각마다 어떤 우선순위로 선택을 내려야 할지 결정한다. 이에 대한 직관을 얻기 위해서는 예제 입력이나 그 외의 작은 입력을 손으로 몇 개 풀어보는 것을 추천
- 어떤 방식이 동작할 것 같으면 두 가지 조건을 증명해보자. (탐욕적 선택 속성, 최적 부분 구조)
예시 문제들
- 백준 1931번 회의실 배정
- 백준 11399번 ATM
'algorithm class' 카테고리의 다른 글
| 레드 블랙 트리란? (4) | 2022.03.24 |
|---|---|
| 알고리즘(Algorithm)이란? (0) | 2020.06.07 |
| [자료구조] 트라이(Trie) (0) | 2020.05.06 |
| [C++] emplace 함수 (2) | 2020.03.05 |
| LCS 알고리즘 (0) | 2020.02.12 |
그리디 알고리즘(Greedy Algorithm)은 "탐욕적인"이라는 뜻의 greedy에서 유래된 알고리즘이다.
다른 말로 "욕심쟁이 기법" 이라고도 부르는데
만약 여러 노드를 갖는 그래프에서 A노드 -> B노드까지의 경로를 탐색하려 할 때 모든 경로를 고려하지 않고
단지, 현재의 위치(노드)에서 가장 최적의 경로(예를 들면 에지의 가중치가 작은) 를 도착지까지 매 순간마다 가장 좋은 방법만을 선택하는 방법이다.

다익스트라 알고리즘도 그리디 알고리즘의 한 예시인데
간단히 설명하자면, 한 노드를 시작점으로 출발해 목적지에 연결될 때 까지 현재 연결된 노드로부터
연결된 에지들의 가중치 중 최소만을 선택하는 방법을 말한다. (사이클이 생기지 않는 선에서)
만약 위 그림에서 노드 1->6 까지의 최단 거리를 구하는 문제를 다익스트라 알고리즘을 통해 풀어보자면,

맨 처음 우리가 선택할 수 있는 경로는 1->2, 1->3 둘 뿐이다.
우린 "탐욕적인" 방법을 선택하였기 때문에 둘 중 가중치가 더 적은 1->2 에지를 선택하게 된다.

2번 노드에 도착했기 때문에 이제 2번 노드와 연결된 에지들도 고려해야 한다.
이제 1->3, 2->5, 2->4 총 3가지의 에지들이 있는데, 이 중 가장 최단인 1->3 에지를 선택하게 된다.

이제 3번 노드를 획득했고,
우리가 알고 있는 에지들은 2->5, 2->4, 3->5, 3->4 가 있어서 가장 최단인 2->5 에지를 선택한다.
이런 방법을 통해 최단 경로를 구하게 되면

1->2->5->6으로 이어지는 거리 5의 최단거리를 구할 수 있게 된다.
하지만 이는 잘 알려진 다익스트라 알고리즘 안의 그리디 알고리즘이고
실제로 우리가 문제를 풀 때에는 그리디를 생각해내기 쉽지 않고, 많은 경우 그리디로 풀면 되겠다! 싶은데
실제로 풀면 최적해를 찾지 못하여 틀리는 경우도 있고, 풀었으나 왜 이게 최적인지 확실하게 증명하지 못하는 경우가 많다.
따라서 적용하기 전 그리디 알고리즘의 정당성을 검증해 봐야 한다.
그리디 알고리즘의 두 가지 증명
1. 탐욕적 선택 속성(greedy choice property)
2. 최적 부분 구조(optimal substructure)
1. 탐욕적 선택 속성(greedy choice property) 은 동적 계획법처럼 답의 모든 부분을 고려하지 않고 탐욕적으로만
선택하더라도 최적해를 구할 수 있다는 것을 의미한다.
즉, 앞에서 탐욕적인 선택을 해서 "손해"를 볼 일이 없어야 한다.
2. 최적 부분 구조(optimal substructure)는 탐욕적으로 선택한 매 순간의 결과가 전체 문제의 최적이어야 한다.
만약 눈앞에 보이는 빠른 길만을 이용해 도착점에 도달했는데, 시작점에서 도착점으로 바로 가는 지름길이 더 빠른경우 탐욕적으로 선택하면 안된다는 것이다.
그리디 알고리즘의 어려움
많은 고수분들은 그리디 알고리즘을 어렵다고 한다.
실제로 대회에서도 그리디 알고리즘으로 생각되는 문제를 가장 나중에 푼다고도 한다.
그리디 알고리즘은 개념은 간단하지만, 그리디 문제를 막상 마주쳤을 때 문제에 여러 조건이 있기 때문에
바로 "이 부분을 최적화하면 해결할 수 있어!"라고 바로 떠오르지 않고, 심지어 풀이는 직관적이나,
문제에 대한 접근이 직관적이지 않기 때문에 함정에 빠지기 십상이다.
따라서 그리디 알고리즘을 연습할 때는 알고리즘의 정당성을 증명하는 과정을 항상 연습하는 것이 필요하다.
그리디 알고리즘과 동적 계획법
입력 조건이 까다롭지 않은 경우 그리디 알고리즘으로 풀 수 있는 문제는 동적 계획법으로 해결 가능하다.
당연하게도 동적 계획법은 모든 경우를 다 고려하기 때문에 메모리나 시간이 초과되지 않는 선에서는 동적 계획법이 더 많이 생각날 것이다.
하지만 역으로 생각해보면 입력 조건이 상당히 까다로운 경우 그리디 알고리즘을 사용하라는 출제자의 힌트가 될 수도 있으니 관련 문제를 많이 풀어봐야 할 것이다.
그리디 알고리즘 풀이 순서
이 풀이 순서는 종만북에 쓰여있는 "탐욕적 알고리즘 레시피" 를 인용하였습니다.
- 문제의 답을 만드는 과정을 여러 조각으로 나눈다.
- 각 조각마다 어떤 우선순위로 선택을 내려야 할지 결정한다. 이에 대한 직관을 얻기 위해서는 예제 입력이나 그 외의 작은 입력을 손으로 몇 개 풀어보는 것을 추천
- 어떤 방식이 동작할 것 같으면 두 가지 조건을 증명해보자. (탐욕적 선택 속성, 최적 부분 구조)
예시 문제들
- 백준 1931번 회의실 배정
- 백준 11399번 ATM
'algorithm class' 카테고리의 다른 글
| 레드 블랙 트리란? (4) | 2022.03.24 |
|---|---|
| 알고리즘(Algorithm)이란? (0) | 2020.06.07 |
| [자료구조] 트라이(Trie) (0) | 2020.05.06 |
| [C++] emplace 함수 (2) | 2020.03.05 |
| LCS 알고리즘 (0) | 2020.02.12 |
