algorithm class
힙 정렬(Heap sort)
suhwanc
2019. 10. 19. 22:17
- 기본 아이디어
-> 버블 정렬과 비슷하다. 1등을 뽑아내고 (최대 힙의 루트), 나머지 원소에서 1등을 계속 뽑아내면 정렬이다. - 버블 정렬과 다른점
-> 1등을 뽑아낸 뒤, 나머지 원소에서 1등을 뽑을 때 다시 비교할 필요 없이 2등이 자동으로 1등이 된다. (루트 원소를 제거 한 후 -> 힙을 유지하는 방식)
힙이란?
- 힙의 성질
- 1. 리프 노드를 제외한 모든 노드는 자식이 반드시 둘이다.
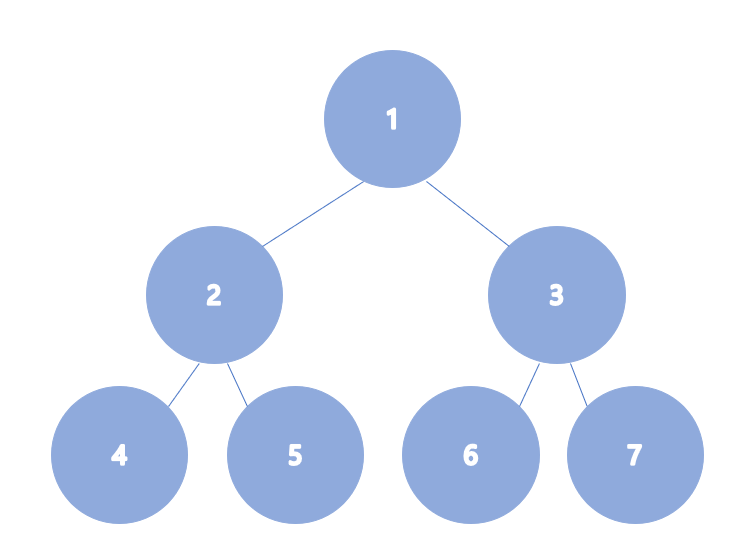
- 완전 이진트리에서 리프 노드가 어떤 노드 이후부터 모두 생략된 형태이다.
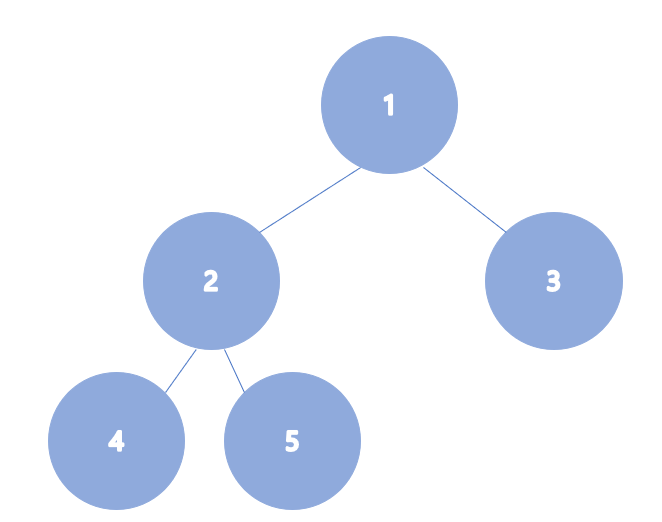
- 트리를 배열로 표현할 수 있다. (노드의 왼쪽 자식 : node * 2, 오른쪽 자식 : node * 2 + 1)
| 1 | 2 | 3 | 4 | 5 |
-
최대 힙 (max heap)
- 정의 : 각 노드들이 (루트 포함) 자식들보다 큰 힙
- 최대 힙에서 루트 원소 제거
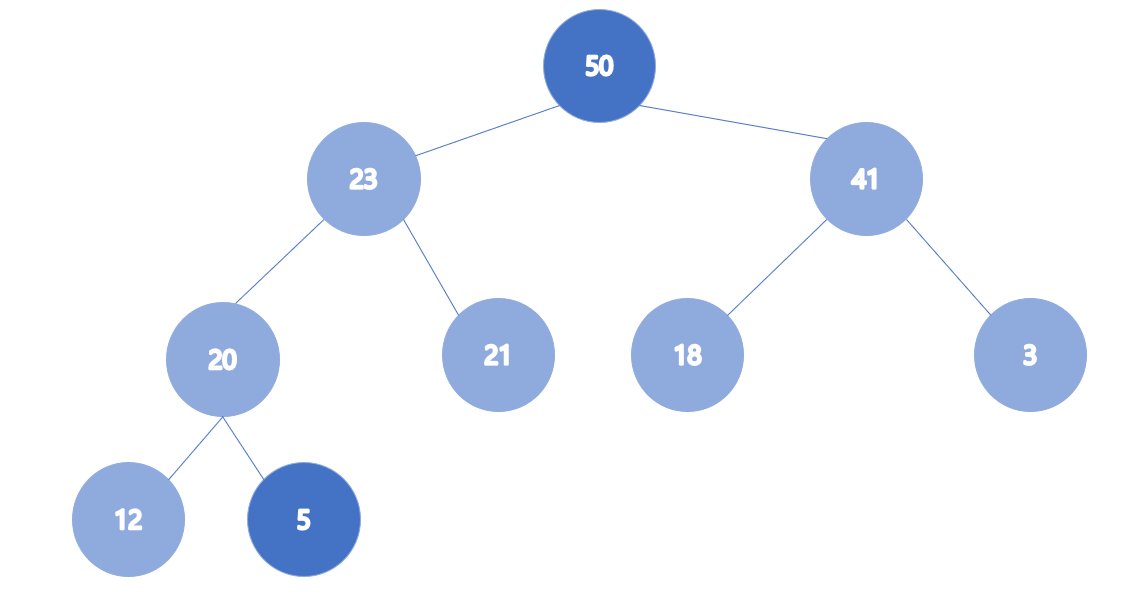
여기서 루트가 제거되면, 이 자리에 가장 마지막 원소를 옮기고,
옮겨진 마지막 노드와 원래 노드의 두 자식, 총 세 값을 비교한다.
그 중 가장 큰 원소가 올라가고, 이 과정을 계속 반복한다. 결과는
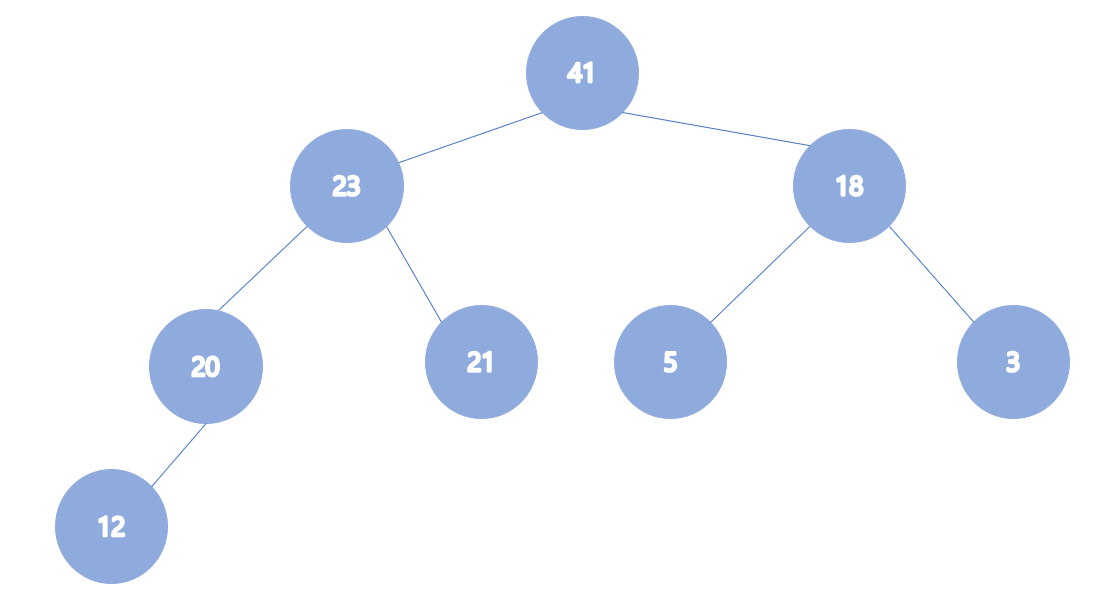
-
최대 힙을 만드는 방법
- Case 1
그렇다면 이미 만들어진 힙을 조정하는 것 말고 직접 처음부터 최대 힙을 만들어보자!
- heap_arr = [2,4,6,0,1,3,5]

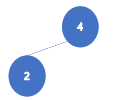
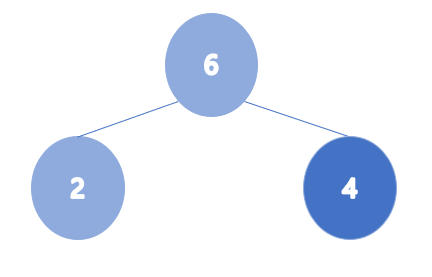
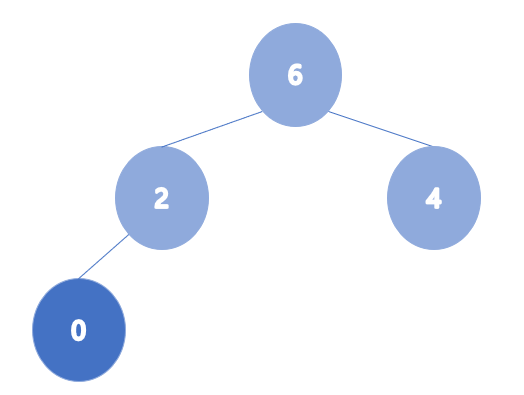
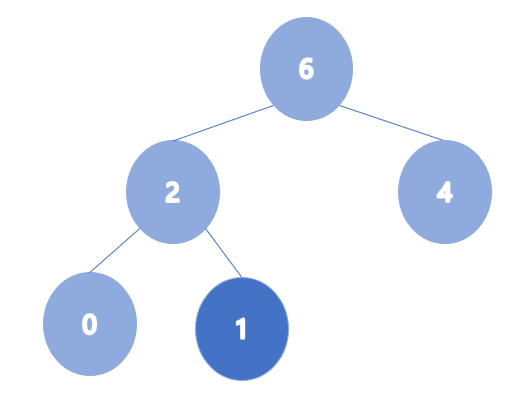
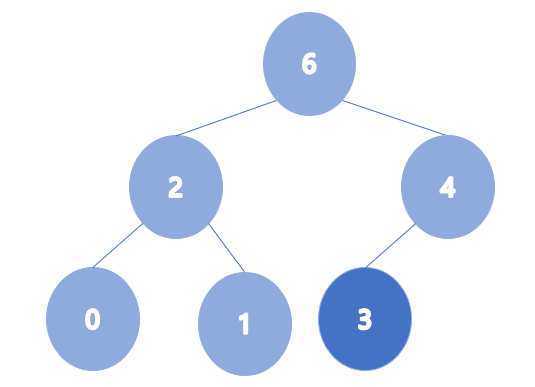
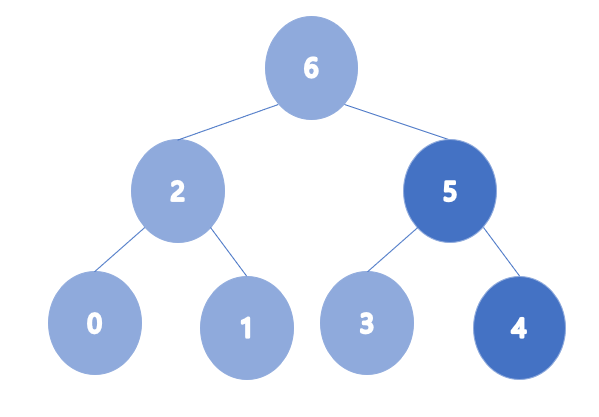
이렇게 힙을 하나 하나 차례대로 넣으면서 만드는 방법이 있고
힙은 배열로 표현할 수 있으므로 처음 상태에서 max heap으로 고쳐나가는 방법도 있다.
- Case 2 : 배열의 형태대로 힙을 만들고 max heap 형태로 수정
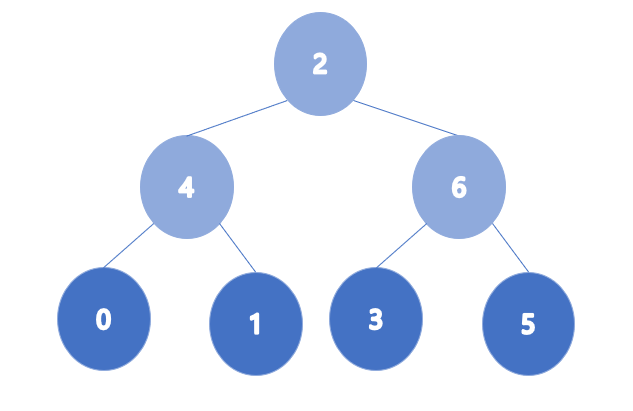
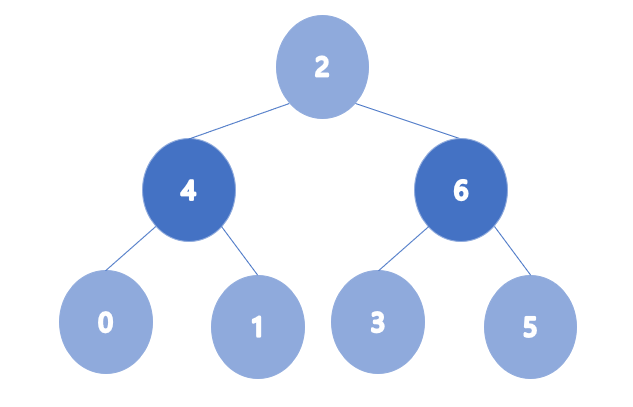
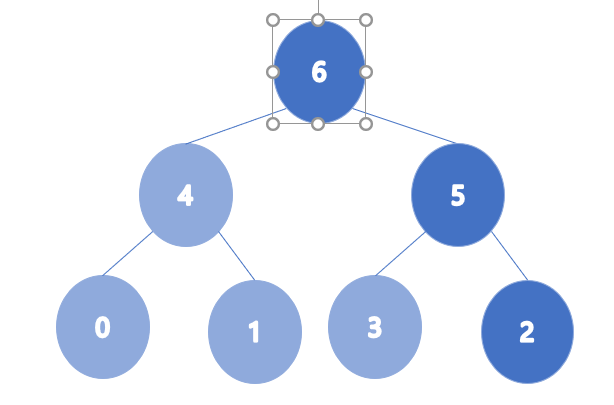
-
시간 복잡도
1. 처음 비어 있는 힙에 차례대로 원소를 삽입하는데 걸리는 시간
-> log1 + log2 + ... + logn = O(nlogn)
2. 두 힙을 계속 병합하는데 걸리는 시간
-> T(n) = 2T(n/2) + logn = O(n)
(logn 은 맨 위 루트노드를 만드는것에 대한 시간입니다!)
T(n) <= 2(cn/2 - log(n/2) - 2log2) + log n
= cn - 2logn + 2log2 - 4log2 + logn
= cn - logn - 2log2 <= cn - logn - 2log2
따라서 O(n)의 시간복잡도이다